خطای نمونه گیری
- afshinsafaee
- مرداد 26, 1404
- بدون دیدگاه
در آمار و روش تحقیق خطای نمونه گیری عبارتست از اختلاف بین آماره ای که از نمونه محاسبه می شود و پارامتر جامعه.
در نمودارهای زیر خطای نمونه گیری برای میانگین نمایش داده شده است. در نمودار سمت چپ فاصله بین میانگین نمونه و پارامتر جامعه کمتر از نمودار سمت راست است؛ بنابراین، خطای نمونه گیری کمتر است.
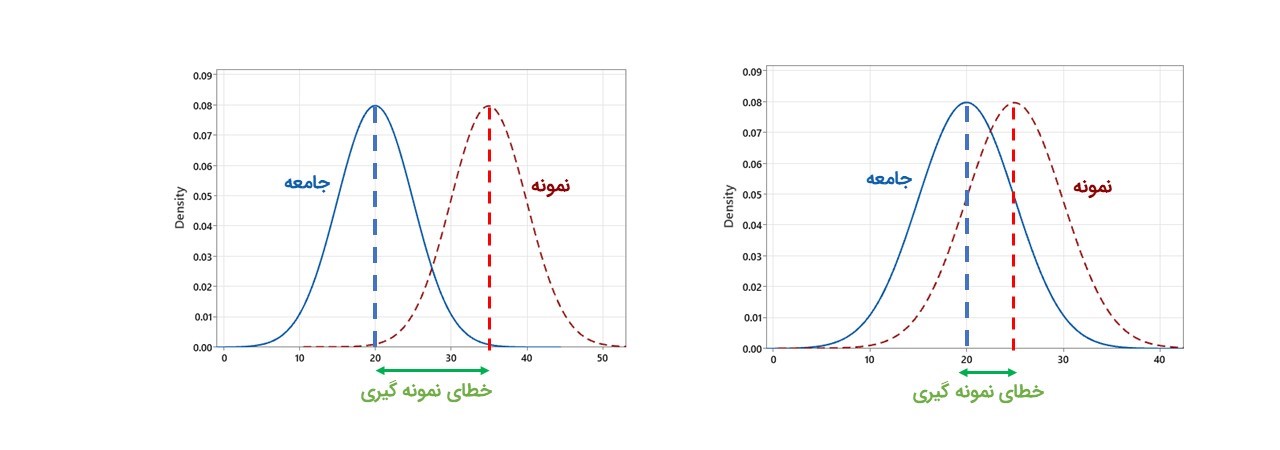
خطای نمونه گیری باعث می شود نمونه تصویر دقیقی از جامعه ارائه نکند و هر چه این خطا بیشتر باشد توان پژوهش و توانایی تحلیل های آماری جهت تعیین تفاوتهای بین گروهها یا توصیف ارتباط بین متغیرها کاهش می یابد.
معمولا خطای نمونه گیری در نمونه های کوچک بزرگتر است و با افزایش حجم نمونه کاهش می یابد.
علل بروز خطای نمونه گیری
خطای نمونه گیری ممکن است دو دلیل داشته باشد:
1) نوسانات (پراکندگی) تصادفی (Random Variation)
2) نوسانات (پراکندگی) نظام مند (Systematic Variation)
در ادامه هر کدام از این دلایل را به تفصیل بررسی می کنیم:
نوسانات تصادفی
نوسانات تصادفی تفاوتی مورد انتظار است و زمانی اتفاق می افتد که فرد اعضاء مختلف یک نمونه را بررسی کند. اگر برای توصیف نمونه، از میانگین استفاده می شود، مقادیر افراد در آن نمونه همگی دقیقا مشابه میانگین نمونه نخواهند بود.
مقادیر خاص هر واحد پژوهش متفاوت از مقدار میانگین نمونه است. این اختلاف تصادفی است، چرا که احتمالا مقدار هر واحد پژوهش در جهتی مختلف تغییر می کند. برخی از مقادیر بیشتر و برخی کمتر از میانگین نمونه هستند. بنابراین، مقادیر به طور تصادفی در اطراف میانگین پخش می شوند. با افزایش حجم نمونه، تغییرپذیری کلی در مقادیر نمونه کاهش می یابد، بدین ترتیب که مقادیر به میانگین نمونه نزدیک تر می شوند. با افزایش حجم نمونه میانگین نمونه با احتمال بیشتری مقداری مشابه با میانگین جمعیت خواهد بود.
فرض کنید میخواهیم میانگین قد دانشآموزان یک دبیرستان را اندازهگیری کنیم.
ما بهجای اندازهگیری همهی دانشآموزان (کل جمعیت)، از ۳۰ نفر بهطور تصادفی نمونه میگیریم.
حتی اگر نمونهگیری کاملاً تصادفی و بدون خطا انجام شود، قد دانشآموزان در این گروه ۳۰ نفری دقیقاً یکسان نخواهد بود. یکی ۱۶۵ سانتیمتر است، یکی ۱۷۰، یکی ۱۵۸، و …. این اختلافها حول میانگین نمونه پخش میشوند؛ مثلا اگر میانگین این ۳۰ نفر ۱۶۷ سانتیمتر باشد، برخی بالاتر و برخی پایینتر قرار دارند.
این پراکندگی ناشی از شانسِ انتخاب افراد متفاوت است، نه به خاطر روش اشتباه یا ابزار معیوب. اگر حجم نمونه را از ۳۰ نفر به ۳۰۰ نفر افزایش دهیم، میانگین نمونه خیلی بیشتر به میانگین واقعی کل جمعیت نزدیک میشود و تغییرات تصادفی کاهش پیدا میکند.
نوسانات نظام مند
نوسانات نظام مند یا تورش نظام مند محصول انتخاب واحدهایی است که مقادیر اندازه گیری آنها در برخی جنبه های خاص از جمعیت متفاوت است یا تغییر کند. از آنجایی که واحدها ویژگی مشترکی دارند، مقادیر آنها گرایش دارد شبیه به مقادیر سایرین در نمونه باشد، اما در برخی موارد در کل متفاوت از مقادیر جمعیت است. این مقادیر به طور تصادفی اطراف میانگین جمعیت تغییر نمی کند. بیشترین نوسان و تغییر از میانگین در جهتی یکسان است که نظام مند می باشد. همه مقادیر در نمونه ممکن است گرایش داشته باشند که کمتر یا بیشتر از میانگین جامعه باشند.
به دلیل واریانس نظام مند، میانگین نمونه از میانگین جامعه متفاوت است. مقدار این اختلاف، خطای نمونه گیری است.
نکته: معیارهای خروج در نمونه گیری باعث ایجاد تورش نظام مند در نمونه می شوند و در نتیجه، باعث خطای نمونه گیری می شود.
در مطالعات تجربی (آزمایشی) معیارهای انتخاب نمونه اغلب زیاد است و اغلب موجب می شود خطای نمونه گیری افزایش یافته و روایی بیرونی پژوهش کاهش می یابد.
نکته: اگر روش انتخاب نمونه دارای تورش نظام مند باشد، افزایش حجم نمونه خطای نمونه گیری را کاهش نمی دهد.
وقتی تورش نظام مند در یک پژوهش آزمایشی (تجربی) اتفاق بیفتد، می تواند پژوهشگر تصور کند مداخله باعث ایجاد تفاوت شده است، در حالیکه در واقع مقادیر حتی بدون مداخله نیز متفاوت بوده اند. معمولا این وضعیت به خاطر تاثیر متقابل تورش نظام مند یا مداخله رخ می دهد.
فرض کنید همان پژوهش بررسی میانگین قد دانشآموزان یک دبیرستان را انجام میدهیم؛ اما این بار، بهجای انتخاب تصادفی دانشآموزان، فقط از تیم بسکتبال مدرسه نمونه میگیریم. قد اعضای تیم بسکتبال بهطور میانگین بسیار بلندتر از بقیهی دانشآموزان مدرسه است. بنابراین، نتیجهی ما بهطور سیستماتیک (همه در یک جهت) بزرگتر از میانگین قد واقعی کل مدرسه خواهد بود. این تفاوت دیگر ناشی از شانس و پراکندگی تصادفی نیست، بلکه از روش انتخاب نمونه میآید که یک گروه خاص و غیرنماینده از جمعیت را انتخاب کرده است.
نکته کلیدی اینکه حتی اگر حجم نمونه را بهجای ۳۰ نفر، ۳۰۰ نفر بگیریم، تا زمانی که همهشان از تیم بسکتبال باشند، میانگین ما همچنان بهشدت بالاتر از واقعیت خواهد بود.
