همبستگی دو رشته ای نقطه ای با استفاده از SPSS

معرفی

یک همبستگی دو رشته ای نقطه ای (Point-Biserial Correlation) برای اندازه گیری قدرت و جهت ارتباطی که بین یک متغیر پیوسته و یک متغیر دو وضعیتی وجود دارد، استفاده می شود. این یک مورد خاص از همبستگی حاصل‌ضرب-گشتاور پیرسون (Pearson’s product-moment correlation) است که زمانی اعمال می شود که دو متغیر پیوسته داشته باشید، در حالی که در این مورد یکی از متغیرها در مقیاس دو وضعیتی (dichotomous) اندازه گیری می شود.

برای مثال، می‌توانید از یک همبستگی دو رشته ای نقطه‌ای استفاده کنید تا بفهمید آیا رابطه‌ای بین حقوق کارمندان‌، و جنسیت وجود دارد یا نه؟. در این مثال، متغیر پیوسته شما «حقوق» و متغیر دو وضعیتی شما «جنسیت» با دو دسته «مرد» و «زن» خواهد بود.

این آموزش به شما نشان می‌دهد که چگونه با استفاده از SPSS، یک همبستگی دو رشته ای نقطه ای را انجام دهید، و همچنین نحوه تفسیر و گزارش نتایج این آزمون را نشان می‌دهد. با این حال، قبل از اینکه شما را با این روش آشنا کنیم، باید فرضیات مختلفی را که داده‌های شما باید رعایت کنند تا یک همبستگی Point-Biserial به شما نتیجه معتبری بدهد، بدانید. در ادامه به این فرضیات می پردازیم.

فرضیات

هنگامی که تصمیم می‌گیرید داده‌های خود را با استفاده از همبستگی دو رشته ای نقطه ای آنالیز کنید، باید ابتدا مطمئن شوید که آیا داده‌های شما واقعاً می‌توانند با استفاده از همبستگی دو رشته ای نقطه ای آنالیز شوند یا نه؟. شما باید این کار را انجام دهید. زیرا تنها زمانی مناسب است که از یک همبستگی Point-Biserial استفاده کنید که داده های شما از پنج فرض لازم برای این همبستگی عبور کند تا یک نتیجه معتبر به شما بدهد. در عمل، بررسی این پنج فرض کمی زمانبر خواهد بود. با این حال، کار سختی نیست.

فرض شماره 1:

یکی از دو متغیر شما باید در مقیاس پیوسته اندازه گیری شود. نمونه‌هایی از متغیرهای پیوسته عبارتند از: زمان (اندازه‌گیری شده بر حسب ساعت)، هوش (اندازه‌گیری شده با استفاده از امتیاز IQ)، نمره امتحان (اندازه‌گیری شده از 0 تا 20)، وزن (اندازه‌گیری شده بر حسب کیلوگرم)، و غیره.

فرض شماره 2:

متغیر دیگر شما باید دو وضعیتی باشد. نمونه هایی از متغیرهای دو وضعیتی شامل جنسیت (دو گروه: مرد یا زن)، وضعیت اشتغال (دو گروه: شاغل یا بیکار)، سیگاری (دو گروه: بله یا خیر) و غیره است.

فرض شماره 3:

برای متغیر پیوسته برای هر دسته از متغیر دو وضعیتی، نباید هیچ داده ی پرتی وجود داشته باشد. می توانید با استفاده از نمودارهای جعبه ای (boxplots)، داده های پرت را آزمایش کنید.

فرض شماره 4:

متغیر پیوسته شما برای هر دسته از متغیر دو وضعیتی باید تقریباً به صورت نرمال توزیع شود. شما می توانید این نرمال بودن توزیع را با استفاده از آزمون نرمال بودن Shapiro-Wilk بررسی کنید.

فرض شماره 5:

متغیر پیوسته شما باید واریانس های برابری برای هر دسته از متغیر دو وضعیتی داشته باشد. شما می توانید این را با استفاده از آزمون برابری واریانس لوون (Levene’s test of equality of variances) آزمایش کنید.

با استفاده از SPSS می توانید فرضیات #3، #4 و #5 را بررسی کنید. فقط به یاد داشته باشید که اگر آزمون های آماری را بر اساس این فرضیات به درستی اجرا نکنید، نتایجی که هنگام اجرای یک همبستگی دو رشته ای نقطه ای به دست می آورید ممکن است معتبر نباشند.

در بخش بعدی، روش SPSS را برای انجام یک همبستگی دو رشته ای نقطه ای با فرض اینکه هیچ فرض گفته شده، نقض نشده است، نشان می‌دهیم. ابتدا، مثالی را که برای توضیح روش همبستگی Point-Biserial در SPSS استفاده کرده ایم، را بیان می کنیم.

مثال و تنظیمات در SPSS

یک آژانس تبلیغاتی می خواهد تعیین کند که آیا رابطه ای بین جنسیت و مشارکت در تبلیغات اینترنتی وجود دارد یا خیر. برای دستیابی به این هدف، آگهی اینترنتی به 20 مرد و 20 زن نشان داده شد و از آنها خواسته شد تا یک نظرسنجی آنلاین را تکمیل کنند که میزان مشارکت آنها با تبلیغات را اندازه گیری می کند. نظرسنجی آنلاین منجر به یک امتیاز مشارکت کلی گردید. پس از جمع آوری داده ها، آژانس تبلیغاتی تصمیم می گیرد از SPSS برای بررسی رابطه بین مشارکت و جنسیت استفاده کند.

بنابراین، در SPSS دو متغیر در Variable View ایجاد شد: جنسیت که دارای دو دسته (“males” و “females” (“مرد” و “زن”)) و مشارکت (یعنی یک امتیاز واحد برای هر فرد بر اساس نتایج نظرسنجی آنلاین که سطح مشارکت آنها با تبلیغات اینترنتی را نشان می دهد).

توجه: این دو متغیر باید به درستی در Variable View تنظیم شوند تا یک همبستگی دو رشته ای نقطه ای اجرا شود (و از خطر اجرای تصادفی همبستگی حاصل‌ضرب-گشتاور پیرسون جلوگیری شود).

روش آزمون در SPSS

روش Correlate > Bivariate… در زیر به شما نشان می دهد که چگونه داده های خود را با استفاده از همبستگی دو رشته ای نقطه ای در SPSS برای ورژن های مختلف از نرم افزار آنالیز کنید. البته به شرطی که هیچ یک از پنج فرض گفته شده در بخش فرضیات، نقض نشده باشد. پس از این روش، نحوه تفسیر نتایج این آزمایش را به شما نشان می دهیم.

مرحله (1)

همانطور که در زیر نشان داده شده است، روی

Analyze > Correlate > Bivariate…

در منوی اصلی کلیک کنید:

برای ورژن 27 و 28

 

برای ورژن 26 و قبل

 

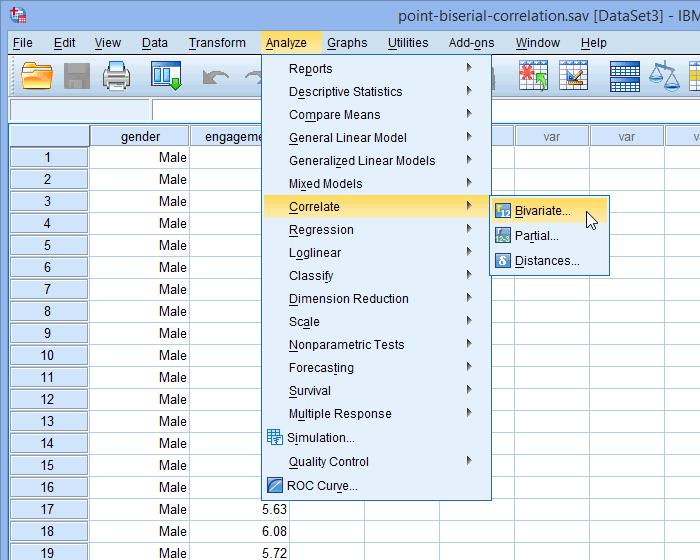
همانطور که در زیر نشان داده شده است پنجره ی Bivariate Correlations نمایش داده می شود:

 

برای ورژن 27 و 28

 

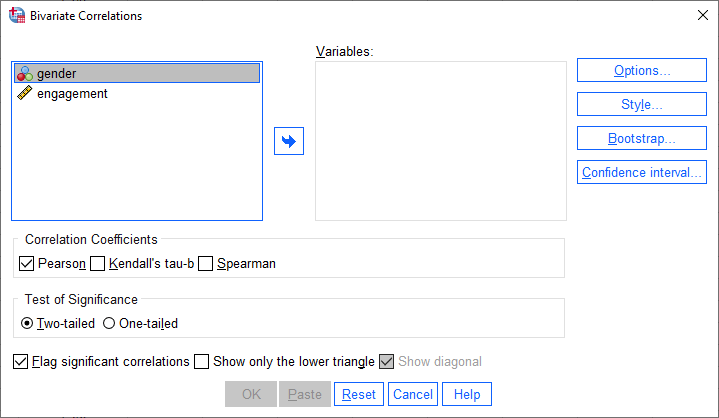
برای ورژن 26 و قبل

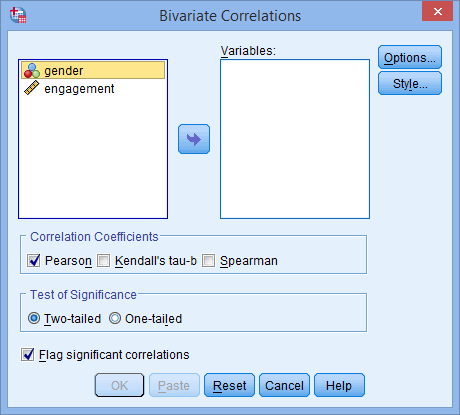
مرحله (2)

با کشیدن و رها کردن یا با کلیک بر روی دکمه فلش ، متغیرها و را به کادر Variables منتقل کنید. در نهایت با صفحه‌ای مشابه تصویر زیر مواجه خواهید شد:

 

برای ورژن 27 و 28

 

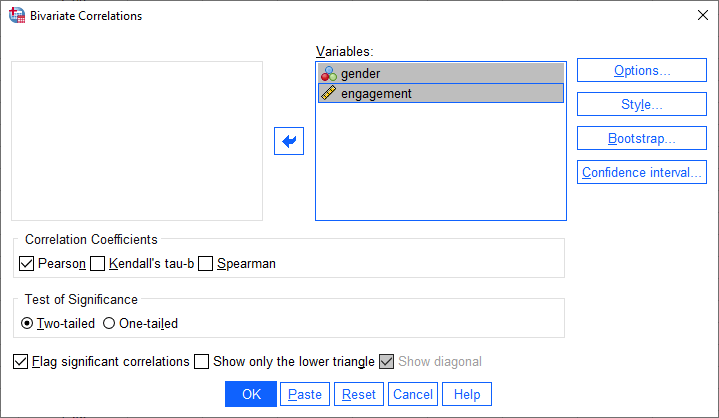
برای ورژن 26 و قبل

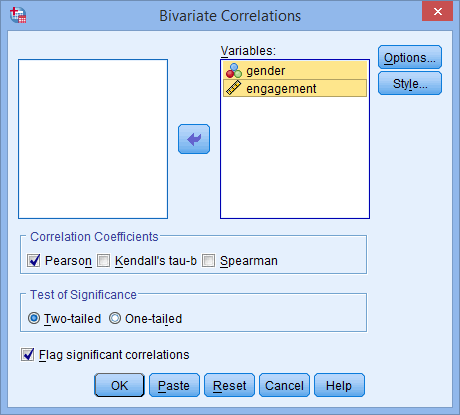
مرحله (3)

همانطور که در زیر نشان داده شده است، اطمینان حاصل کنید که چک باکس Pearson در ناحیه – Correlation Coefficients– علامت زده شده باشد (اگرچه این گزینه به طور پیش فرض در SPSS انتخاب شده است):

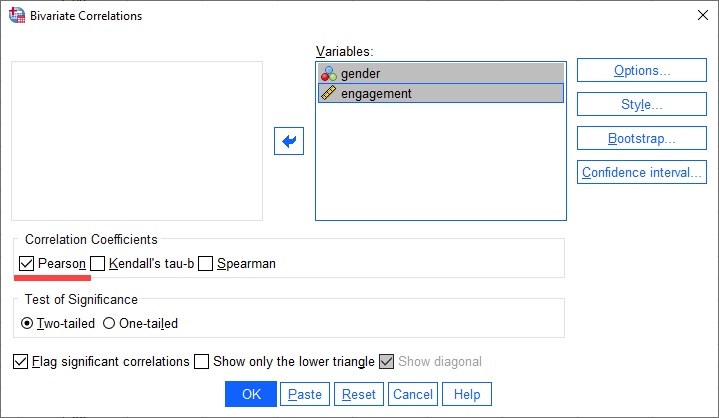
مرحله (4)

برای ورژن 27 و 28

همانطور که در زیر نشان داده شده است، چک باکس Show only the bottom triangle را انتخاب کنید و سپس تیک چک باکس Show diagonal را بردارید:

 

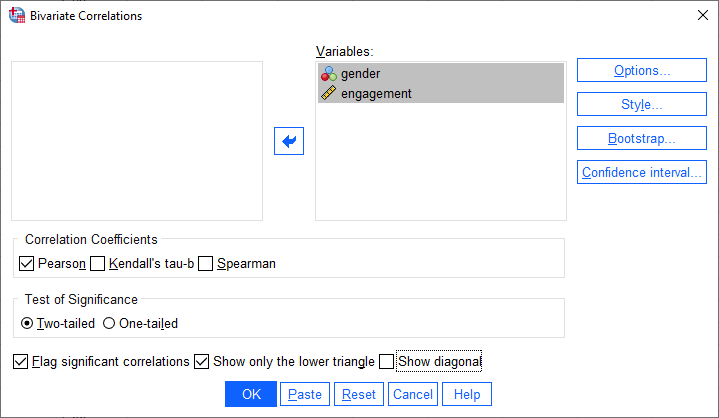
برای ورژن 26 و قبل

بر روی دکمه Options کلیک کنید. اگر می‌خواهید برخی از توصیف‌ها را ایجاد کنید، می‌توانید این کار را در اینجا با کلیک کردن بر روی کادر مربوطه در قسمت –Statistics– انجام دهید. سپس بر روی دکمه Continue کلیک کنید.

مرحله (5)

بر روی دکمه OK کلیک کنید تا خروجی تولید گردد.

تفسیر نتایج همبستگی دو رشته ای نقطه ای

اگر داده‌های شما از فرضیات #3 (بدون نقاط پرت)، #4 (توزیع نرمال) و #5 (واریانس‌های برابر) که قبلاً در بخش فرضیات توضیح داده شد، عبور کند، فقط باید جدول Correlations (همبستگی‌ها) را تفسیر کنید. به یاد داشته باشید که اگر داده‌های شما با هر یک از این فرضیات با شکست مواجه شود، خروجی‌ای که از روش همبستگی دو رشته ای نقطه ای دریافت می کنید، دیگر معتبر نخواهد بود.

با این حال، در این آموزش، ما فقط بر نتایج حاصل از روش همبستگی دو رشته ای نقطه ای تمرکز می‌کنیم، با این فرض که داده‌های شما تمام فرضیات مربوطه را برآورده می‌کنند. بنابراین، اگر روش همبستگی دوسری نقطه‌ای را در SPSS اجرا کنید، جدول Correlations در زیر نمایش داده می‌شود:

برای ورژن 27 و 28

 

برای ورژن 26 و قبل

 

جدول همبستگی در واقع بیان می کند که “همبستگی پیرسون” اجرا شده است زیرا همبستگی دو رشته ای نقطه ای به سادگی یک مورد خاص از همبستگی حاصل‌ضرب-گشتاور پیرسون است، که در آن شما دو متغیر پیوسته دارید، در حالی که در همبستگی دو رشته ای نقطه ای یکی از متغیرها در مقیاس دو وضعیتی اندازه گیری می شود. بنابراین، اگر یک همبستگی پیرسون را به جای همبستگی Point-Biserial اجرا کرده اید، نگران نباشید. تا زمانی که داده های خود را به درستی در Variable View تنظیم کرده باشید، یک همبستگی دو رشته ای نقطه ای به طور خودکار توسط SPSS اجرا می شود.

جدول Correlations ضریب همبستگی Point-Biserial، مقدار معنی داری و حجم نمونه را که محاسبه بر اساس آن است، نشان می دهد. در این مثال، می‌توانیم ببینیم که ضریب همبستگی دو رشته ای نقطه ای، r_pb، -.358 است و این از نظر آماری معنادار است (p=.023).

گزارش همبستگی Point-Biserial

در مثال بالا، بهتر است نتایج را به صورت زیر ارائه کنید:

برای تعیین رابطه بین مشارکت در یک آگهی اینترنتی و جنسیت، یک همبستگی دو رشته ای نقطه ای اجرا شد. بین مشارکت و جنسیت همبستگی منفی وجود داشت که از نظر آماری معنی دار بود

r_pb=-.358, n=40, p=.023

 

مطالب زیر را هم از دست ندهید:

ضریب همبستگی رتبه‌ای اسپیرمن (Spearman rank-order correlation coefficient) با استفاده از SPSS

همبستگی جزئی (Partial Correlation) با استفاده از SPSS

همبستگی اسپیرمن در Minitab

ضریب همبستگی تاوی- بی کندال (Kendall’s Tau-b correlation coefficient) با استفاده از SPSS

گامای گودمن و کروسکال (Goodman and Kruskal’s gamma) با استفاده از SPSS

آزمون H کروسکال-والیس (H Kruskal-Wallis) با استفاده از Stata

Afshin Safaee (@afshinsafaee.official)