تجزیه و تحلیل رگرسیون پواسون با استفاده از SPSS Statistics

معرفی

از رگرسیون پواسون (Poisson Regression) برای پیش‌بینی یک متغیر وابسته استفاده می‌شود که از تعدادی داده‌ با یک یا چند متغیر مستقل تشکیل شده است. متغیری که می خواهیم پیش بینی کنیم، متغیر وابسته (یا گاهی اوقات پاسخ، متغیر نتیجه، هدف یا معیار) نامیده می شود. متغیرهایی که برای پیش‌بینی مقدار متغیر وابسته استفاده می‌کنیم، متغیرهای مستقل (یا گاهی اوقات متغیرهای پیش‌بینی‌کننده، توضیحی یا رگرسیون) نامیده می‌شوند. برخی از مثال‌هایی که می‌توان از رگرسیون پواسون استفاده کرد در زیر توضیح داده شده‌اند:

مثال شماره 1:

می توانید از رگرسیون پواسون برای بررسی تعداد دانش آموزان تعلیق شده توسط مدارس در واشنگتن در ایالات متحده بر اساس عوامل پیش بینی کننده مانند جنسیت (دختر و پسر)، نژاد (سفید پوست، سیاه سیاه پوست، و سرخپوست)، زبان (انگلیسی زبان اول آنهاست، انگلیسی زبان اول آنها نیست) و وضعیت توانی (معلول و سالم) استفاده کنید. در اینجا، «تعداد دانش آموزان تعلیق شده» متغیر وابسته است، در حالی که «جنس»، «نژاد»، «زبان» و «وضعیت توانی» همگی متغیرهای مستقل اسمی هستند.

مثال شماره 2:

می توانید از رگرسیون پواسون برای بررسی تعداد دفعاتی که افراد در بازپرداخت اقساط وام های خود در یک دوره پنج ساله کوتاهی کرده اند، استفاده کنید. این رگرسیون بر اساس پیش بینی هایی مانند وضعیت شغلی (شاغل، بیکار)، حقوق سالانه، سن (بر حسب سال)، جنسیت (مرد و زن) انجام می شود. در اینجا، «تعداد اقساط پرداختی» متغیر وابسته است، در حالی که «وضعیت شغلی» و «جنسیت» متغیرهای مستقل اسمی و «حقوق سالانه»، «سن» متغیرهای مستقل پیوسته هستند.

با انجام رگرسیون پواسون، می‌توانید تعیین کنید که کدام یک از متغیرهای مستقل (در صورت وجود) تأثیر آماری معنی‌داری بر متغیر وابسته شما دارند. برای متغیرهای مستقل طبقه‌ای (categorical independent)، می‌توانید درصد افزایش یا کاهش تعداد یک گروه را تعیین کنید. مثلاً مرگ و میر در میان «کودکان» سوار شده بر ترن هوایی در مقابل گروه دیگر مثلاً مرگ و میر در میان «بزرگ‌سالان» سوار شده بر ترن هوایی. برای متغیرهای مستقل پیوسته، می‌توانید تفسیر کنید که چگونه یک واحد افزایش یا کاهش در آن متغیر با درصد افزایش یا کاهش تعداد متغیر وابسته شما مرتبط است.

این آموزش به شما نشان می دهد که چگونه رگرسیون پواسون را با استفاده از SPSS Statistics انجام دهید، و همچنین نتایج این آزمون را تفسیر و گزارش کنید. با این حال، قبل از اینکه شما را با این روش آشنا کنیم، باید فرضیات مختلفی را که داده های شما باید رعایت کنند تا رگرسیون پواسون به شما نتیجه معتبری بدهد، بدانید. در ادامه به این فرضیات می پردازیم.

فرضیات

هنگامی که تصمیم می‌گیرید داده‌های خود را با استفاده از رگرسیون پواسون تجزیه و تحلیل کنید، باید بررسی کنید که آیا داده‌های شما می توانند با استفاده از رگرسیون پواسون تجزیه و تحلیل شوند یا نه؟. شما باید این کار را انجام دهید. زیرا تنها زمانی استفاده از رگرسیون پواسون مناسب است که داده های شما از پنج فرضی که برای رگرسیون پواسون لازم است تا یک نتیجه معتبر را به شما ارائه دهد، “عبور کند”. در عمل، بررسی این پنج فرض کمی زمان بر خواهد بود. با این حال، ضروری است که این کار را انجام دهید.

فرض شماره 1:

متغیر وابسته شما باید از داده های شمارشی (count data) تشکیل شده باشد. داده‌های شمارشی با داده‌های اندازه‌گیری شده در سایر انواع رگرسیون معروف متفاوت است. به عنوان مثال، رگرسیون خطی (linear) و رگرسیون چندگانه (multiple) به متغیرهای وابسته نیاز دارند که در مقیاس “پیوسته” (continuous) اندازه گیری می شوند. رگرسیون لجستیک دو جمله ای به (binomial logistic) یک متغیر وابسته نیاز دارد که در مقیاس ” دو وضعیتی” (dichotomous) اندازه گیری شود. رگرسیون ترتیبی (ordinal) به یک متغیر وابسته نیاز دارد که در مقیاس “ترتیبی” (ordinal) اندازه گیری می شود و رگرسیون لجستیک چند جمله ای (multinomial logistic) به یک متغیر وابسته نیاز دارد که در مقیاس “اسمی” (nominal) اندازه گیری شود. در مقابل، متغیرهای شمارشی به داده‌های عدد صحیح نیاز دارند که باید صفر یا بیشتر باشند. به زبان ساده، یک عدد صحیح را به عنوان یک عدد “کل” در نظر بگیرید (به عنوان مثال، 0، 1، 5، 8، 354، 888، 23400، و غیره). همچنین، از آنجایی که داده‌های شمارشی باید «مثبت» باشند (یعنی شامل مقادیر صحیح «غیر منفی» باشند)، نمی‌توانند از مقادیر «منفی» تشکیل شوند. علاوه بر این، گاهی اوقات پیشنهاد می شود که رگرسیون پواسون فقط زمانی انجام شود که تعداد میانگین کم باشد (به عنوان مثال، کمتر از 10). در مواردی که تعداد زیادی شمارش وجود دارد، نوع دیگری از رگرسیون ممکن است مناسب تر باشد (به عنوان مثال، رگرسیون چندگانه، رگرسیون گاما، و غیره).

نمونه‌هایی از متغیرهای شمارشی عبارتند از: تعداد پروازهای با تاخیر بیش از سه ساعت در فرودگاه‌ها، تعداد دانش‌آموزانی که توسط مدارس تعلیق شده‌اند، تعداد دفعاتی که مردم در بازپرداخت اقساط کوتاهی کرده‌اند.

فرض شماره 2:

شما یک یا چند متغیر مستقل دارید که می توانند در مقیاس پیوسته، ترتیبی یا اسمی/دو وضعیتی اندازه گیری شوند. متغیرهای ترتیبی و اسمی / دو وضعیتی را می توان به طور کلی به عنوان متغیرهای طبقه ای دسته بندی کرد.

نمونه‌هایی از متغیرهای پیوسته عبارتند از: زمان (اندازه‌گیری شده بر حسب ساعت)، هوش (اندازه‌گیری شده با استفاده از آزمون IQ)، نمره امتحان (اندازه‌گیری شده از 0 تا 20) و وزن (اندازه‌گیری شده بر حسب کیلوگرم). نمونه‌هایی از متغیرهای ترتیبی شامل موارد لیکرت (مثلاً مقیاس 7 درجه‌ای از «کاملاً موافقم» تا «کاملاً مخالفم. نمونه هایی از متغیرهای اسمی عبارتند از جنسیت (به عنوان مثال، دو گروه – مرد و زن – که به عنوان یک متغیر دو وضعیتی نیز شناخته می شود)، قومیت (به عنوان مثال، سه گروه: قفقازی، آفریقایی آمریکایی و اسپانیایی) و حرفه (به عنوان مثال، چهار گروه: جراح، پزشک ، پرستار، دندانپزشک). به یاد داشته باشید که متغیرهای ترتیبی و اسمی / دو وضعیتی را می توان به طور کلی به عنوان متغیرهای طبقه ای دسته بندی کرد.

فرض شماره 3:

مشاهدات شما باید استقلال داشته باشند. این بدان معناست که هر مشاهده مستقل از مشاهدات دیگر است. یعنی یک مشاهده نمی تواند هیچ اطلاعاتی در مورد مشاهده دیگر ارائه دهد. این یک فرض بسیار مهم است. یک روش برای آزمایش امکان استقلال مشاهدات، مقایسه خطاهای مبتنی بر مدل استاندارد با خطاهای قوی برای تعیین اینکه آیا تفاوت های زیادی وجود دارد یا خیر.

فرض شماره 4:

توزیع شمارش ها (مشروط به مدل) از توزیع پواسون پیروی می کند. یکی از پیامدهای این امر این است که تعداد مشاهده شده و مورد انتظار باید برابر باشند. اساساً این به این معناست که مدل، تعداد مشاهده شده را به خوبی پیش بینی می کند. این را می‌توان با روش‌های مختلفی آزمایش کرد، اما یکی از روش‌ها محاسبه تعداد مورد انتظار و ترسیم آن‌ها با شمارش‌های مشاهده‌شده برای مشاهده مشابه بودن آنهاست.

فرض شماره 5:

میانگین و واریانس مدل یکسان است. این نتیجه فرض شماره 4 است. که توزیع پواسون وجود دارد. برای توزیع پواسون، باید واریانس برابر با میانگین باشد. اگر این فرض را برآورده کنید، شما پراکندگی یکسان (equidispersion) دارید. با این حال، اغلب اینطور نیست. روش های مختلفی وجود دارد که می توانید برای ارزیابی پراکندگی بیش از حد (overdispersion) استفاده کنید. یک روش ارزیابی Pearson dispersion statistic است.

با استفاده از SPSS Statistics می توانید فرضیات #3، #4 و #5 را بررسی کنید. قبل از فرضیات شماره 3، 4 و 5، ابتدا باید فرضیات شماره 1 و 2 بررسی شوند. فقط به یاد داشته باشید که اگر آزمون های آماری را بر اساس این فرضیات به درستی اجرا نکنید، نتایجی که هنگام اجرای رگرسیون پواسون به دست می آورید ممکن است معتبر نباشند.

همچنین، اگر داده‌های شما فرض شماره 5 را نقض کنند (که در هنگام انجام رگرسیون پواسون بسیار رایج است)، ابتدا باید بررسی کنید که آیا «پراکندگی بیش از حد پواسون» دارید یا خیر. پراکندگی ظاهری پواسون جایی است که شما مدل را به درستی مشخص نکرده اید به طوری که به نظر برسد داده ها پراکندگی بیش از حد دارند. بنابراین، اگر مدل پواسون شما در ابتدا فرض  پراکندگی یکسان را نقض می کند، ابتدا باید تعدادی تنظیمات را در مدل پواسون خود انجام دهید تا بررسی کنید که واقعاً پراکندگی بیش از حد است. این مستلزم آن است که شش مدل/داده خود را بررسی کنید: (1) آیا مدل پواسون شما شامل همه پیش بینی های مهم است؟ (ب) آیا داده های شما شامل داده های پرت می باشد؟ (ج) آیا رگرسیون پواسون شما شامل تمام عبارات تعامل مرتبط است؟ (د) آیا هیچ یک از پیش بینی کننده های شما نیاز به تغییر دارد؟ (ه) آیا مدل پواسون شما به داده های بیشتری نیاز دارد و/یا داده های شما خیلی کم است؟ و (f) آیا مقادیر گمشده ای دارید که به طور تصادفی گم نشده اند (are not missing at random (MAR))؟

در بخش زیر، روش SPSS Statistics را برای انجام یک رگرسیون پواسون با فرض اینکه هیچ فرض گفته شدهدر بالا نقض نشده است، نشان می‌دهیم. ابتدا مثالی را که در این آموزش استفاده شده معرفی می کنیم.

مثال و تنظیمات در SPSS Statistics

مدیر تحقیقات یک دانشگاه کوچک می‌خواهد ارزیابی کند که آیا تجربه یک دانشگاهی (academic) و زمان در دسترس برای انجام تحقیقات بر تعداد مقالات چاپ شده آنها تأثیر می‌گذارد یا خیر. لذا از نمونه تصادفی 21 نفری از دانشگاهیان جهت شرکت در پژوهش خواسته شده است: 10 نفر از دانشگاهیان با تجربه و 11 نفر از دانشگاهیان کم تجربه. تعداد ساعت‌هایی که در 12 ماه گذشته برای تحقیق صرف کرده‌اند و تعداد مقالات چاپ شده توسط آنها ثبت می‌شود.

برای تنظیم این طرح مطالعه در SPSS Statistics، ما سه متغیر ایجاد کردیم: (1) no_of_publications، که تعداد مقالات چاپ شده ی است که دانشگاهیان در مجلات معتبر در 12 ماه گذشته منتشر کرده‌اند. (2) experience_of_academic، که نشان می دهد که آیا دانشگاهی باتجربه است (یعنی 10 سال یا بیشتر در دانشگاه کار کرده است، و بنابراین به عنوان “آکادمیک با تجربه” طبقه ای می شود) یا اخیراً یک دانشگاهی شده است و (3) no_of_weekly_hours، که تعداد ساعاتی است که هر هفته برای کار بر روی یک پروژه صرف می شود.

روش آزمون در SPSS Statistics

13 مرحله زیر به شما نشان می دهد که چگونه داده های خود را با استفاده از رگرسیون پواسون در SPSS Statistics تجزیه و تحلیل کنید، البته زمانی که هیچ یک از پنج فرض گفته شده در بخش قبلی، نقض نشده است. در پایان این 13 مرحله، ما به شما نشان می دهیم که چگونه نتایج حاصل از رگرسیون پواسون را تفسیر کنید.

مرحله (1)

همانطور که در زیر نشان داده شده است، روی

Analyze > Generalized Linear Models > Generalized Linear Models…

در منوی اصلی کلیک کنید:

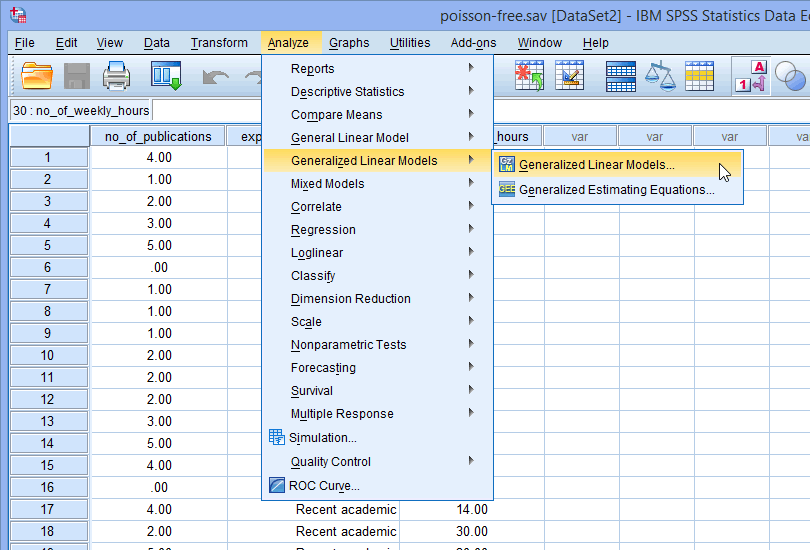
در زیر با پنجره ی Generalized Linear Models روبرو خواهید شد:

مرحله (2)

مانند شکل زیر، Poisson loglinear را در قسمت Counts انتخاب کنید:

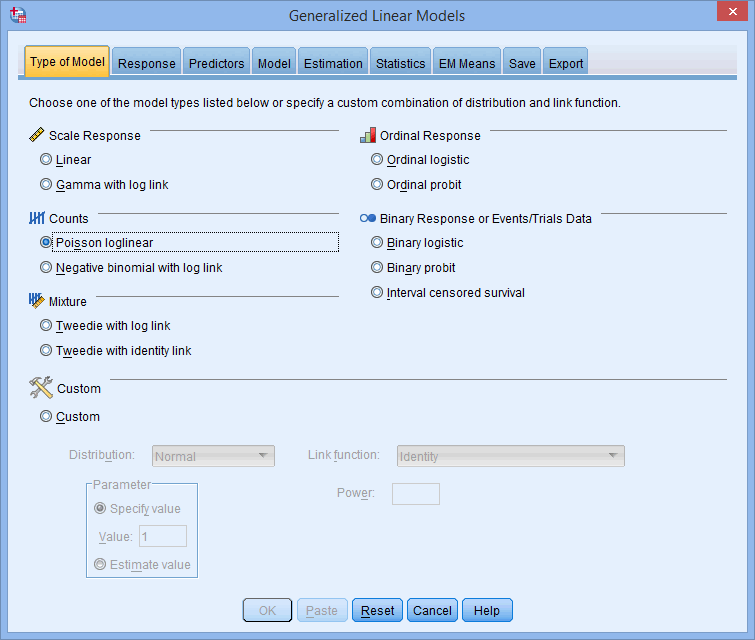
توجه: در حالت استاندارد، برای انجام رگرسیون پواسون، Poisson loglinear را در ناحیه Counts انتخاب می کنند، با این حال می توانید با انتخاب Custom در ناحیه Custom و سپس با استفاده از گزینه های Distribution:، Link و Parameter نوع مدل پواسون را که می خواهید اجرا کنید، مشخص کنید.

مرحله (3)

تب Response را انتخاب کنید. با پنجره ی زیر روبرو خواهید شد:

مرحله (4)

متغیر وابسته خود، no_of_publications، را با استفاده از دکمه فلش ، مانند شکل زیر، به کادر Dependent variable منتقل کنید:

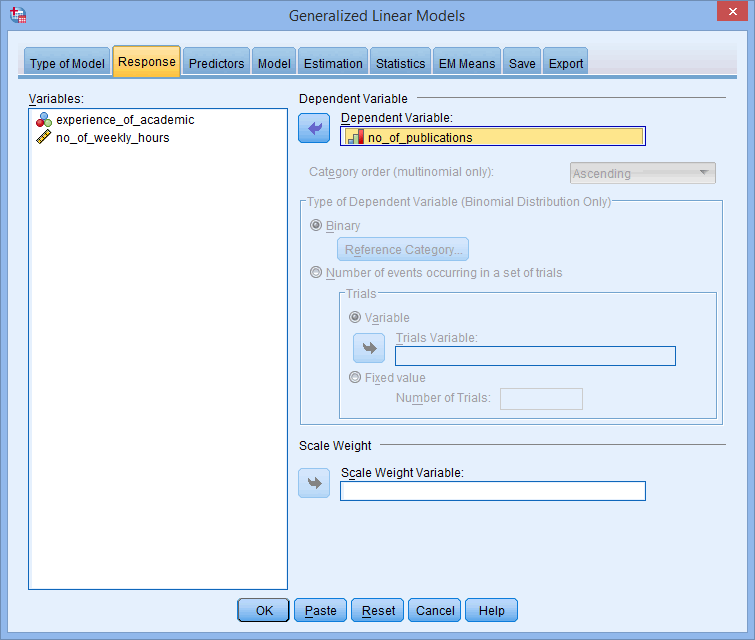
مرحله (5)

تب Predictors را انتخاب کنید. با پنجره ی زیر روبرو خواهید شد:

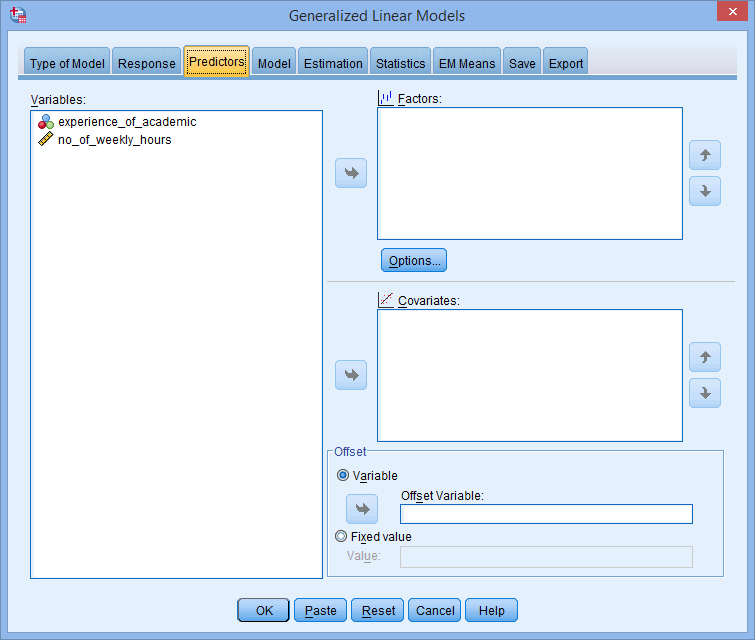
مرحله (6)

متغیر مستقل طبقه ای، experience_of_academic، را به کادر Factors و متغیر مستقل پیوسته، no_of_weekly_hours را به کادر Covariates با استفاده از دکمه‌های فلش ، مانند شکل زیر، منتقل کنید:

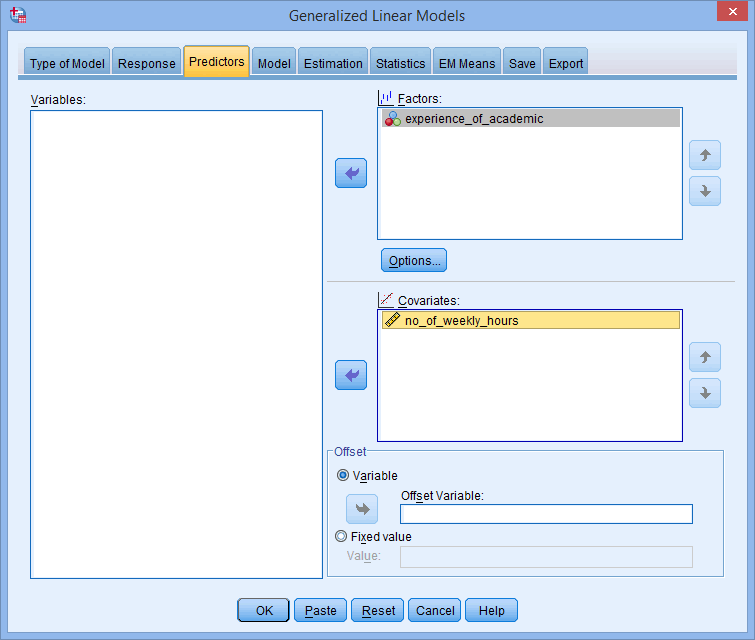
نکته 1: اگر متغیرهای مستقل ترتیبی دارید، باید تصمیم بگیرید که آیا این متغیرها را به عنوان طبقه ای در نظر می گیرید و در کادر Factors وارد می کنید یا به عنوان پیوسته در نظر گرفته و در کادر Covariates وارد می کنید. با این حال آنها را نمی توان به عنوان متغیرهای ترتیبی در رگرسیون پواسون وارد کرد.

نکته 2: معمولا متغیرهای مستقل پیوسته را در کادر Covariates وارد می کنند، با این حال می توان به جای آن متغیرهای مستقل ترتیبی را وارد کرد. که در این صورت متغیر مستقل ترتیبی شما به عنوان پیوسته در نظر گرفته می شود.

نکته 3: اگر بر روی دکمه Options کلیک کنید پنجره ی زیر ظاهر می شود:

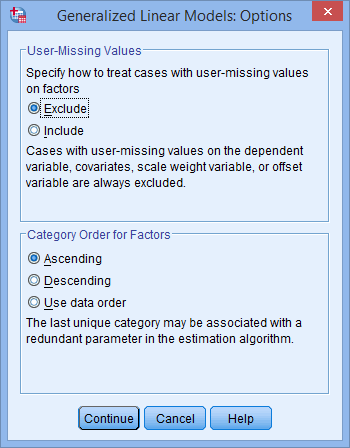
در ناحیه –Category Order for Factors– می توانید گزینه هایی بین Ascending, Descending و Use data order را انتخاب کنید. اینها مفید هستند. زیرا SPSS Statistics به طور خودکار متغیرهای طبقه ای شما را به متغیرهای ساختگی تبدیل می کند. تفسیر خروجی از رگرسیون پواسون برای هر یک از گروه‌های متغیرهای طبقه‌ای شما کمی دشوار است. اگر با متغیرهای ساختگی آشنایی دارید، با ایجاد تغییرات در گزینه‌های موجود در ناحیه -Category Order for Factors- می‌توانید تفسیر خروجی را آسان‌تر کنید.

مرحله (7)

تب Model را انتخاب کنید. با پنجره ی زیر روبرو خواهید شد:

مرحله (8)

پیش‌فرض را در ناحیه – Build Term(s) – نگه دارید و متغیرهای مستقل طبقه‌ای و پیوسته، experience_of_academic و no_of_weekly_hours را از کادر Factors and Covariates به کادر Model با استفاده از دکمه فلش منتقل کنید، همانطور که در زیر نشان داده شده است:

نکته 1: در پنجره ی ، مدل پواسون خود را می سازید. به طور خاص، شما تعیین می کنید که چه اثرات اصلی دارید (گزینه )، و همچنین آیا انتظار دارید بین متغیرهای مستقل شما تعاملی وجود داشته باشد یا نه (گزینه ). اگر مشکوک هستید که بین متغیرهای مستقل خود تعاملی دارید، گنجاندن این متغیرها در مدل شما نه تنها برای بهبود پیش بینی مدل شما مهم است، بلکه برای جلوگیری از مسائل مربوط به پراکندگی بیش از حد (فرض شماره 5)، مهم است.

ما در اینجا یک مثال بسیار ساده را برای یک مدل با یک اثر اصلی (بین متغیرهای مستقل طبقه ای و پیوسته، experience_of_academic و no_of_weekly_hours) ارائه داده ایم. با این حال می توانید به راحتی مدل های پیچیده تر را با استفاده از فاکتوریل ، ، وارد کنید. همه گزینه‌های و در ناحیه –Build Term(s)– به نوع اثرات اصلی (main effects) و تعاملاتی (interactions) که در مدل خود دارید، بستگی دارد.

نکته 2: همچنین می‌توانید با افزودن آنها به کادر Term در ناحیه –Build Nested Term– عبارت‌های تودرتو (nested terms) را در مدل خود بسازید. ما در این مدل اثرات تودرتو نداریم، اما سناریوهای زیادی وجود دارد که ممکن است اصطلاحات تودرتو در مدل خود داشته باشید.

مرحله (9)

تب را انتخاب کنید. با پنجره ی زیر روبرو خواهید شد:

مرحله (10)

گزینه های پیش فرض را انتخاب کنید.

توجه: تعدادی گزینه مختلف وجود دارد که می توانید در منطقه –Parameter Estimation– انتخاب کنید، از جمله توانایی انتخاب متفاوت: (الف) روش پارامتر مقیاس (به عنوان مثال، یا به جای در کادر Scale Parameter Method) که ممکن است برای مقابله با مسائل پراکندگی بیش از حد در نظر گرفته شود. (ب) ماتریس کوواریانس (به عنوان مثال، Robust estimator به جای Model-based estimator در ناحیه Covariance Matrix)، که گزینه بالقوه دیگری برای مقابله با مسائل پراکندگی بیش از حد ارا ئه می‌کند.

همچنین تعدادی مشخصات وجود دارد که می‌توانید در ناحیه – Iterations- برای مقابله با مسائل عدم همگرایی (non-convergence) در مدل پواسون خود ایجاد کنید.

مرحله (11)

تب Statistics را انتخاب کنید. با پنجره ی زیر روبرو خواهید شد:

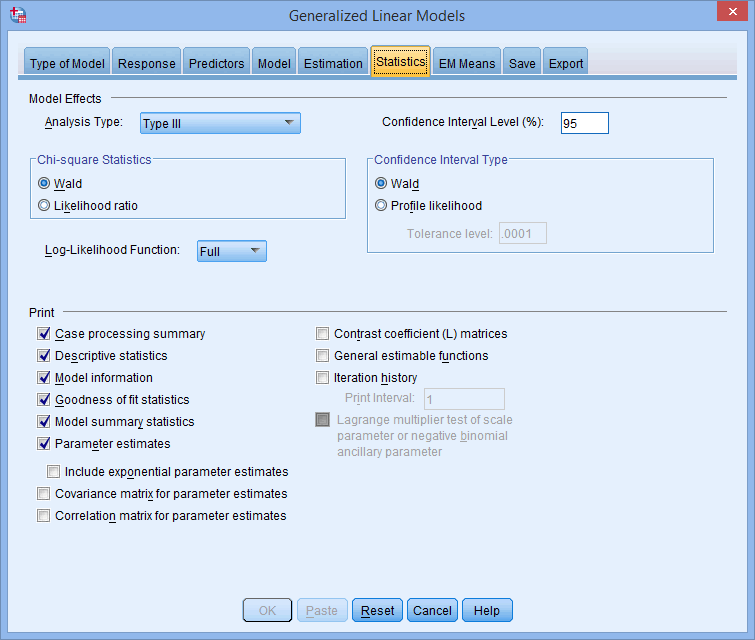
مرحله (12)

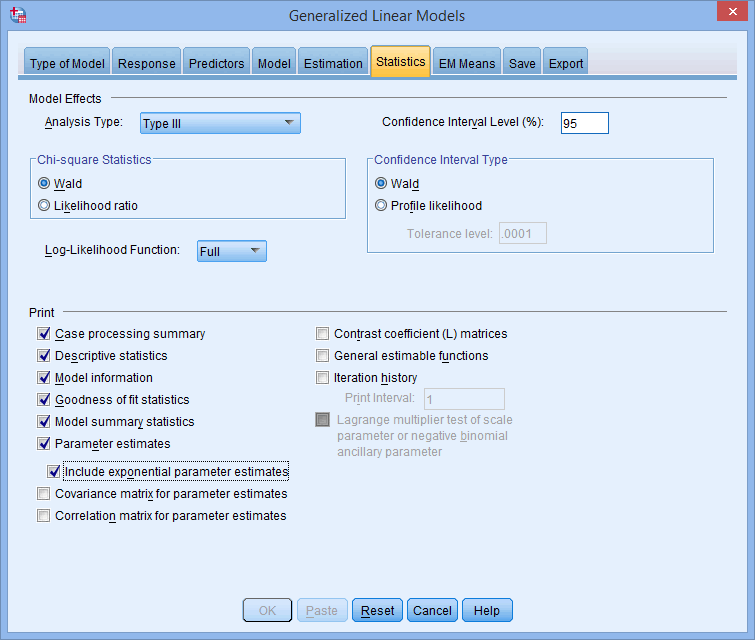
همانطور که در زیر نشان داده شده است، Include exponential parameter estimates را در ناحیه Print انتخاب کنید:

نکته 1: در قسمت ، شما می توانید بین نسبت Wald و Likelihood بر اساس عواملی مانند اندازه نمونه انتخاب کنید.

در ناحیه ، آزمون ضریب لاگرانژ (Lagrange multiplier test) می‌تواند برای تعیین اینکه آیا مدل پواسون برای داده‌های شما مناسب است یا نه (اگرچه این را نمی‌توان با استفاده از روش رگرسیون پواسون اجرا کرد) مفید باشد.

نکته 2: همچنین می توانید طیف گسترده ای از گزینه های دیگر را از تب های EM Means و Save انتخاب کنید. اینها شامل گزینه‌هایی می‌شوند که هنگام بررسی تفاوت‌های بین گروه‌های متغیرهای طبقه‌ای شما و همچنین آزمایش فرضیات رگرسیون پواسون،مهم هستند.

مرحله (13)

بر روی دکمه OK کلیک کنید. با انجام تمام این مراحل، خروجی تولید می شود.

تفسیر و گزارش خروجی رگرسیون پواسون

SPSS Statistics تعداد زیادی جدول خروجی برای تحلیل رگرسیون پواسون ایجاد می کند. در این بخش، هشت جدول اصلی مورد نیاز برای درک نتایج خود از روش رگرسیون پواسون را به شما نشان می دهیم، با این فرض که هیچ فرض گفته شده در بخش قبلی نقض نشده است.

اطلاعات مدل و متغیر (Model and variable information)

(1) اولین جدول در خروجی جدول Model Information است (مانند شکل زیر). این تأیید می کند که متغیر وابسته (dependent variable)، “تعداد مقالات چاپ شده ” (Number of publications) می باشد. توزیع احتمال (probability distribution)، “پواسون” است و تابع پیوند (link function)، لگاریتم طبیعی است (به عنوان مثال، “Log”). اگر رگرسیون پواسون را روی داده های خود اجرا می کنید، نام متغیر وابسته متفاوت خواهد بود، اما توزیع احتمال و تابع پیوند یکسان خواهد بود.

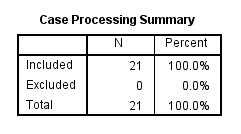
(2) جدول دوم، Case Processing Summary (خلاصه پردازش پرونده)، به شما نشان می دهد که چند مورد (به عنوان مثال، سوژه ها) در تجزیه و تحلیل شما (ردیف “Included”) و چند مورد شامل نشده (ردیف “Excluded”) و همچنین درصد هر دو گنجانده شده است. می‌توانید ردیف «Excluded» را به‌عنوان مواردی (به‌عنوان مثال، سوژه ها) که یک یا چند مقدار گمشده دارند، در نظر بگیرید. همانطور که در زیر می بینید، 21 سوژه در این تجزیه و تحلیل وجود داشت که هیچ سوژه ای حذف نشد (یعنی مقادیر گمشده ای وجود نداشت).

(3) جدول Categorical Variable Information (اطلاعات متغیر طبقه‌ای)، تعداد و درصد موارد (به عنوان مثال، سوژه ها) را در هر گروه از هر متغیر طبقه‌ای مستقل در تحلیل شما برجسته می‌کند. در این تحلیل، تنها یک متغیر مستقل طبقه ای (همچنین به عنوان “factor” شناخته می شود) وجود دارد که experience_of_academic بود. می بینید که گروه ها از نظر تعداد بین دو گروه نسبتاً متعادل هستند (یعنی 10 در مقابل 11). اندازه های بسیار نامتعادل گروه می تواند در تناسب مدل مشکلاتی ایجاد کند، اما می بینیم که در اینجا مشکلی وجود ندارد.

(4) جدول Continuous Variable Information (اطلاعات متغیر پیوسته) می تواند یک بررسی ابتدایی از داده ها برای هر گونه مشکل ارائه دهد، اما نسبت به سایر آمارهای توصیفی که می توانید قبل از اجرای رگرسیون پواسون به طور جداگانه اجرا کنید، مفیدتر است. بهترین چیزی که می توانید از این جدول بدست آورید این است که درک کنید که آیا ممکن است در تحلیل شما پراکندگی بیش از حد وجود داشته باشد یا نه؟. (به عنوان مثال، فرض شماره 5 رگرسیون پواسون). می توانید این کار را با در نظر گرفتن نسبت واریانس (توان دوم ستون “Std. Deviation”) به میانگین (ستون “Mean”) برای متغیر وابسته انجام دهید. در زیر می توانید این ارقام را مشاهده کنید:

میانگین 2.29 و واریانس 2.81 (1.67758²) است که نسبت 2.81÷2.29=1.23 است. توزیع پواسون نسبت 1 را فرض می کند (یعنی میانگین و واریانس برابر هستند). بنابراین، می‌توانیم ببینیم که قبل از اینکه متغیرهای توضیحی را اضافه کنیم، مقدار کمی ‌پراکندگی بیش از حد وجود دارد. با این حال، زمانی که همه متغیرهای مستقل به رگرسیون پواسون اضافه شده اند، باید این فرض را بررسی کنیم. در بخش بعدی به این موضوع پرداخته می شود.

تعیین میزان تناسب مدل

(5) جدول Goodness of Fit معیارهای زیادی را ارائه می کند که می توان از آنها برای ارزیابی میزان تناسب مدل استفاده کرد. با این حال، ما روی مقدار ستون “Value/df” برای ردیف “Pearson Chi-Square” تمرکز می کنیم که در این مثال 1.108 است، همانطور که در زیر نشان داده شده است:

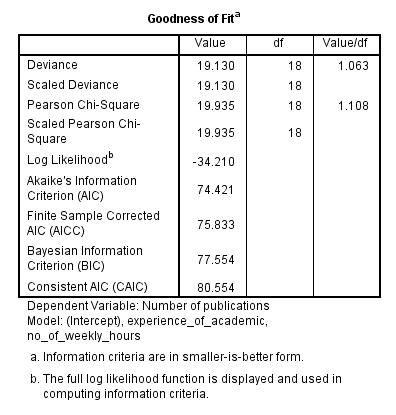
مقدار 1 نشان دهنده پراکندگی یکسان (equidispersion) است در حالی که مقادیر بیشتر از 1 نشان دهنده پراکندگی بیش از حد و مقادیر زیر 1 نشان دهنده عدم پراکندگی است. رایج ترین نوع نقض فرض پراکندگی بیش از حد است. با چنین حجم نمونه کوچکی در این مثال، مقدار 1.108 بعید است که نقض جدی این فرض باشد.

(6) جدول Omnibus Test جایی بین این بخش و بخش بعدی قرار می گیرد. این یک آزمون نسبت احتمال است که نشان می دهد آیا همه متغیرهای مستقل مجموعاً مدل را به مدل عـرض از مبـدا (intercept-only model) بهبود می بخشند یا نه؟ (یعنی بدون هیچ متغیر مستقل اضافه شده). با داشتن همه متغیرهای مستقل در مدل مثال ما، مقدار p برابر با 0.006 (یعنی p = 0.006) داریم که نشان دهنده یک مدل کلی آماری معنی دار است، همانطور که در زیر ستون “Sig.” نشان داده شده است:

اکنون که می‌دانید اضافه کردن همه متغیرهای مستقل، یک مدل آماری معنی دار تولید می کند، می‌خواهید بدانید که کدام متغیرهای مستقل خاص از نظر آماری معنادار هستند. در بخش بعدی به این موضوع پرداخته می شود.

اثرات مدل (Model effects) و معناداری آماری (statistical significance) متغیرهای مستقل

(7) جدول Tests of Model Effects (همانطور که در زیر نشان داده شده است) اهمیت آماری هر یک از متغیرهای مستقل را در ستون “Sig.” نشان می دهد:

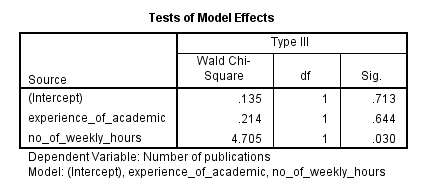
معمولاً هیچ علاقه ای به عرض از مدل وجود ندارد. با این حال، می‌توان دید که تجربه دانشگاهیان (experience of the academic) از نظر آماری معنی‌دار نبود (0.644=p)، اما تعداد ساعات کار در هفته از نظر آماری معنی‌دار بود (0.030=p). این جدول بیشتر برای متغیرهای مستقل طبقه‌ای مفید است، زیرا تنها جدولی است که بر خلاف جدول Parameter Estimates، همانطور که در زیر نشان داده شده است، تأثیر کلی یک متغیر طبقه‌ای را در نظر می‌گیرد:

(8) جدول Parameter Estimates هم تخمین های ضرایب (ستون “B”) رگرسیون پواسون و هم مقادیر توان ضرایب (ستون “Exp(B)”) را ارائه می دهد. این مقادیر توان نشان داده شده را می توان به بیش از یک روش تفسیر کرد و ما در این آموزش یک راه را به شما نشان خواهیم داد. به عنوان مثال، تعداد ساعات کار در هفته را در نظر بگیرید (یعنی ردیف “no_of_weekly_hours”). Exp(B) مقدار توان 1.044 است. این بدان معناست که تعداد مقالات چاپ شده (یعنی تعداد متغیر وابسته) برای هر ساعت کار اضافی در هفته 1.044 برابر بیشتر خواهد بود. راه دیگری برای بیان این موضوع این است که به ازای هر ساعت کار اضافی در هفته، 4.4 درصد افزایش در تعداد مقالات چاپ شده وجود دارد. تفسیر مشابهی را می توان برای متغیر طبقه ای انجام داد.

همه اش را کنار هم بگذار

می توانید نتایج تعداد ساعات کار در هفته را به صورت زیر بنویسید:

یک رگرسیون پواسون برای پیش‌بینی تعداد مقالات چاپ شده ی که یک دانشگاه در 12 ماه گذشته بر اساس تجربه دانشگاهیان و تعداد ساعت‌هایی که یک دانشگاهی در هفته صرف کار بر روی تحقیق می‌کند، اجرا شد. به ازای هر ساعت کار اضافی در هفته بر روی تحقیق، 1.044 (95% فاصله اطمینان (CI)، 1.004 تا 1.085) برابر بیشتر مقالات چاپ شده منتشر شد که دارای یک نتیجه آماری معنی دار، p=.030 می باشد.

 

 

مطالب زیر را هم از دست ندهید:

رگرسیون لجستیک ترتیبی با استفاده از SPSS

رگرسیون چندگانه با استفاده از SPSS

رگرسیون خطی با استفاده از SPSS

Afshin Safaee (@afshinsafaee.official)