ANOVA با اندازه گیری های مکرر با استفاده از SPSS Statistics

پری کرمی
دسامبر 15, 2022
9 دیدگاه ها

ANOVA با اندازه گیری های مکرر با استفاده از SPSS Statistics

مقدمه

یک ANOVA با اندازه گیری های مکرر برای مقایسه سه یا چند میانگین گروهی که در آن شرکت کنندگان در هر گروه یکسان هستند، استفاده می شود. این معمولا در دو حالت اتفاق می افتد: (1) زمانی که شرکت کنندگان چندین بار اندازه گیری می شوند تا تغییرات یک مداخله را مشاهده کنند. یا (2) زمانی که شرکت کنندگان تحت بیش از یک شرط/آزمایش (condition/trial) قرار می گیرند و پاسخ به هر یک از این شرایط می خواهد با هم مقایسه شود.

برای مثال، می‌توانید از ANOVA اندازه‌گیری‌های مکرر استفاده کنید تا متوجه شوید که آیا تفاوتی در مصرف سیگار در بین افراد سیگاری پس از یک برنامه هیپنوتیزم درمانی وجود دارد یا نه؟. (به عنوان مثال، با سه نقطه زمانی: مصرف سیگار بلافاصله قبل، 1 ماه بعد، و 6 ماه پس از هیپنوتیزم درمانی). در این مثال، “مصرف سیگار” متغیر وابسته شما است، در حالی که متغیر مستقل شما “زمان” است (یعنی با سه گروه مرتبط، که در آن هر یک از سه نقطه زمانی یک “گروه مرتبط” در نظر گرفته می شود).

توجه: در حالی که ANOVA اندازه گیری های مکرر زمانی استفاده می شود که شما فقط “یک” متغیر مستقل دارید، اگر “دو” متغیر مستقل دارید باید از ANOVA اندازه گیری های مکرر دو طرفه استفاده کنید.

این آموزش به شما نشان می دهد که چگونه با استفاده از SPSS Statistics یک ANOVA اندازه گیری های مکرر را انجام دهید، و همچنین نتایج این آزمون را تفسیر و گزارش کنید. با این حال، قبل از اینکه شما را با این روش آشنا کنیم، باید فرضیات مختلفی را که داده‌های شما باید رعایت کنند تا ANOVA اندازه‌گیری‌های مکرر به شما نتیجه معتبری بدهد، بدانید. در ادامه به این فرضیات می پردازیم.

فرضیات

وقتی تصمیم می‌گیرید داده‌های خود را با استفاده از ANOVA اندازه‌گیری‌های مکرر تجزیه و تحلیل کنید، باید مطمئن شوید که داده‌هایی که می‌خواهید تجزیه و تحلیل کنید واقعاً می‌توانند با استفاده از ANOVA اندازه‌گیری‌های مکرر تجزیه و تحلیل شوند یا نه؟. زیرا استفاده از ANOVA اندازه گیری های مکرر تنها زمانی مناسب است که داده های شما از پنج فرض لازم برای ANOVA اندازه گیری های مکرر عبور کند تا یک نتیجه معتبر به شما بدهد. در عمل، بررسی این پنج فرض، کمی زمان تجزیه و تحلیل را زیاد میکند. ولی کار سختی نیست.

فرض شماره 1:

متغیر وابسته شما باید در سطح پیوسته اندازه گیری شود (یعنی در سطح فاصله ای (interval) یا نسبتی (ratio)). نمونه‌هایی از متغیرهای پیوسته عبارتند از: زمان (اندازه‌گیری شده بر حسب ساعت)، هوش (اندازه‌گیری شده با استفاده از نمره IQ)، نمره امتحان (اندازه‌گیری شده از 0 تا 20)، وزن (اندازه‌گیری شده بر حسب کیلوگرم)، و غیره.

فرض شماره 2:

متغیر مستقل شما باید حداقل از دو دسته بندی، “گروه های مرتبط” (related groups) یا “جفت همسان” (matched pairs) تشکیل شده باشد. “گروه های مرتبط” نشان می دهد که در هر دو گروه افراد مشابهی وجود دارد. امکان وجود سوژه های یکسان در هر گروه بخاطر این است که هر سوژه در دو نوبت بر روی یک متغیر وابسته اندازه گیری شده است. به عنوان مثال، ممکن است عملکرد 10 نفر را در آزمون املا (متغیر وابسته) قبل و بعد از اینکه آنها تحت یک شکل جدید از روش آموزشی کامپیوتری برای بهبود املا قرار گرفتند، اندازه گیری کرده باشید.

دوست دارید بدانید که آیا آموزش کامپیوتر عملکرد املایی آنها را بهبود می بخشد؟ گروه مرتبط اول شامل سوژه های ابتدایی (قبل از) آموزش املای کامپیوتری و گروه دوم مرتبط از همان سوژه ها، اما پس از آموزش کامپیوتری است. از ANOVA اندازه گیری های مکرر نیز می توان برای مقایسه سوژه ها مختلف استفاده کرد، اما این اغلب اتفاق نمی افتد.

فرض شماره 3:

در گروه‌های مرتبط نباید داده های پرت (outliers) قابل توجهی وجود داشته باشد. داده های پرت صرفاً نقاط داده منفردی در داده‌های شما هستند که از الگوی معمول پیروی نمی‌کنند. مشکل داده های پرت این است که آنها می توانند تأثیر منفی بر ANOVA اندازه گیری های مکرر داشته باشند، تفاوت بین گروه های مرتبط (اعم از افزایش یا کاهش امتیازات متغیر وابسته) را مخدوش می کنند و می توانند دقت نتایج شما را کاهش دهند. خوشبختانه، هنگام استفاده از SPSS Statistics برای اجرای ANOVA اندازه گیری های مکرر بر روی داده های خود، می توانید به راحتی داده های پرت احتمالی را تشخیص دهید.

فرض شماره 4:

توزیع متغیر وابسته در دو یا چند گروه مرتبط باید تقریباً به طور نرمال توزیع شود. در اندازه گیری های مکرر ANOVA فقط به داده های تقریباً نرمال نیاز دارید با این حال، این فرض می تواند کمی نقض شود و همچنان نتایج معتبری ارائه شود. شما می توانید نرمال بودن را با استفاده از تست نرمال Shapiro-Wilk که به راحتی برای استفاده از SPSS Statistics تست می شود، تست کنید.

فرض شماره 5:

که به عنوان کروییت یا کروی بودن (sphericity) شناخته می شود، واریانس تفاوت بین تمام ترکیبات گروه های مرتبط باید برابر باشد. متأسفانه، ANOVA اندازه گیری های مکرر در معرض نقض فرض کروی بودن است، که باعث می شود تست بیش از حد آزاد شود (یعنی منجر به افزایش نرخ خطای نوع I می شود، یعنی ; یعنی احتمال تشخیص یک نتیجه از نظر آماری معنی دار در حالی که وجود ندارد). خوشبختانه، SPSS Statistics آزمایش اینکه آیا داده‌های شما با این فرض مطابقت دارد یا خیر را آسان می‌کند.

با استفاده از SPSS Statistics می توانید فرضیات #3، #4 و #5 را بررسی کنید. قبل از انجام این کار، باید مطمئن شوید که داده های شما با فرضیات #1 و #2 مطابقت دارند، اگرچه برای انجام این کار به SPSS Statistics نیاز ندارید. فقط به یاد داشته باشید که اگر آزمون های آماری را بر اساس این فرضیات به درستی اجرا نکنید، نتایجی که هنگام اجرای ANOVA اندازه گیری های مکرر به دست می آورید ممکن است معتبر نباشند.

در بخش، روش آزمون SPSS Statistics، ما روش آماری SPSS را برای انجام یک ANOVA اندازه گیری های مکرر با فرض اینکه هیچ فرضی نقض نشده است، نشان می دهیم. ابتدا، مثالی را که برای توضیح روش ANOVA اندازه گیری های مکرر در SPSS Statistics استفاده می کنیم، بیان می کنیم.

مثال

یک محقق می خواهد بفهمد که چگونه ورزش ممکن است بیماری قلبی را کاهش دهد. محقق می خواهد روی پروتئینی به نام پروتئین واکنشی C (CRP)تمرکز کند که نشانگر التهاب مزمن در بدن است و با بیماری قلبی مرتبط است: هر چه غلظت CRP بیشتر باشد، خطر ابتلا به بیماری قلبی بیشتر می شود. ورزش منظم خطر ابتلا به بیماری های قلبی را کاهش می دهد. بنابراین، محقق می‌خواهد بداند که آیا ورزش بر غلظت CRP تأثیر دارد یا خیر، زیرا ممکن است نشان دهد که ورزش اثر ضد التهابی دارد.

برای آزمایش این نظریه، محقق 10 سوژه را برای انجام یک برنامه تمرینی 6 ماهه استخدام می کند. غلظت CRP در سه مرحله مختلف در برنامه تمرینی 6 ماهه اندازه گیری می شود: (1) قبل از مداخله (pre). (2) اواسط مداخله در 3 ماهگی (mid). و (3) بلافاصله پس از مداخله (post). این سه نقطه زمانی منعکس کننده سه سطح عامل درون سوژه ای (within-subjects) ما هستند. یعنی یک عامل درون سوژه ای که در مقیاس ترتیبی (ordinal) اندازه گیری می شود، اگرچه یک عامل درون سوژه ای نیز می تواند در مقیاس اسمی (nominal) در هنگام انجام یک ANOVA اندازه‌گیری‌های مکرر یک طرفه اندازه‌گیری شود. متغیر وابسته CRP است که بر حسب mg/L اندازه گیری می شود. یعنی یک متغیر وابسته که در مقیاس پیوسته (continuous) اندازه گیری می شود.

غلظت CRP قبل از مداخله در متغیر crp_pre، غلظت CRP در اواسط مداخله در متغیر crp_mid و غلظت CRP بعد از مداخله در متغیر crp_post ثبت شد. محقق می خواهد بداند که آیا تغییراتی در غلظت CRP در طول زمان وجود دارد یا خیر. در شرایط متغیر، محقق می خواهد بداند که آیا بین سه متغیر crp_pre، crp_mid و crp_post تفاوت وجود دارد یا خیر.

روش تست در SPSS Statistics

روش زیر به شما نشان می‌دهد که چگونه داده‌های خود را با استفاده از ANOVA اندازه‌گیری‌های مکرر در SPSS Statistics تجزیه و تحلیل کنید، البته در صورتی که پنج فرض گفته شده در بخش قبل ، نقض نشده باشند. این روش را در 16 مرحله برای ورژن های مختلف SPSS Statistics به شما نشان می دهیم. در پایان این 16 مرحله، نحوه تفسیر نتایج این آزمون را به شما نشان می دهیم.

SPSS Statistics ورژن 25، 26، 27 و 28

مرحله (1)

همانطور که در زیر نشان داده شده است، روی

Analyze > General Linear Model > Repeated measures…

در منوی اصلی کلیک کنید:

نکته: SPSS Statistics در ورژن 27 ، ظاهر جدیدی را به رابط خود به نام “SPSS Light” معرفی کرد و جایگزین ظاهر قبلی ورژن 26 و ورژن های قبلی شد که “SPSS Standard” نام داشت. بنابراین، اگر ورژن 27 یا 28 SPSS Statistics را دارید، تصاویر زیر خاکستری روشن خواهند بود تا آبی. با این حال، روش یکسان است.

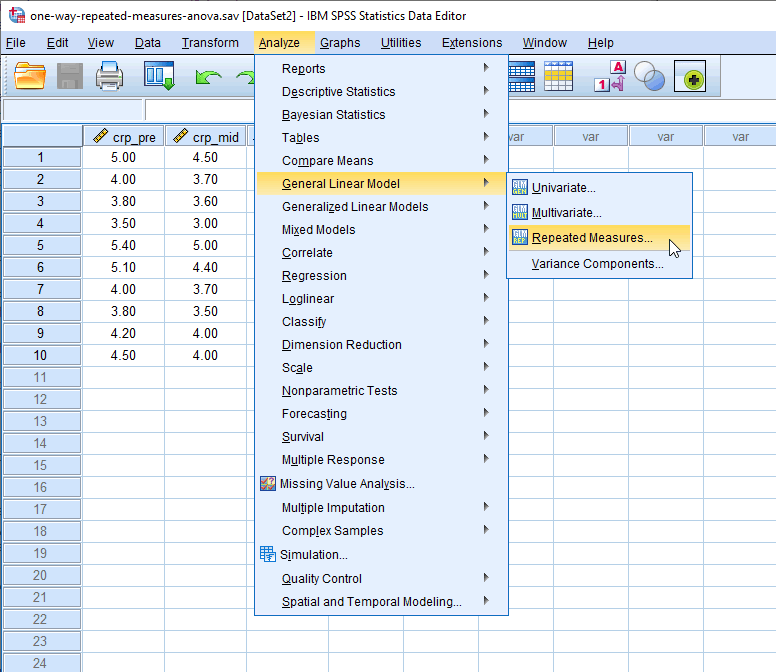
همانطور که در زیر نشان داده شده است، با پنجره ی Repeated Measures Define Factor(s) مواجه خواهید شد:

توضیح: این پنجره جایی است که به SPSS Statistics اطلاع می دهید که سه متغیر – crp_pre، crp_mid و crp_post – سه سطح از فاکتور درون سوژه ای (within-subjects factor)، زمان هستند. بدون انجام این کار، SPSS Statistics فکر می کند که این سه متغیر دقیقاً همان سه متغیر جداگانه هستند.

مرحله (2)

در کادر In-Subject Factor Name ، فاکتور 1 (factor1) را با یک نام معنادارتر برای فاکتور درون سوژه ای خود جایگزین کنید. به عنوان مثال، ما “factor1” را با “time” جایگزین کردیم زیرا این نام عامل درون سوژه ای ما (یعنی زمان) است. سپس تعداد سطوح فاکتور درون سوژه ای خود را در کادر Number of Levels وارد کنید. برای مثال، فاکتور درون سوژه ای ما، زمان، دارای سه سطح است که نشان دهنده سه نقطه زمانی است که متغیر وابسته ما، CRP، اندازه‌گیری شده است (یعنی قبل از مداخله، crp_pre، اواسط مداخله، crp_mid، و پس از مداخله، crp_post). بنابراین، مطابق شکل زیر، عدد 3 را در کادر Number of Levels وارد کردیم:

بر روی دکمه Add کلیک کنید و با صفحه زیر روبرو خواهید شد:

مرحله (3)

در کادر Measure Name نامی را وارد کنید که نشان دهنده نام متغیر وابسته شما باشد. از آنجایی که متغیر وابسته ما CRP است، مطابق شکل زیر “CRP” را وارد می کنیم:

بر روی دکمه Add کلیک کنید و صفحه زیر را مشاهده خواهید کرد:

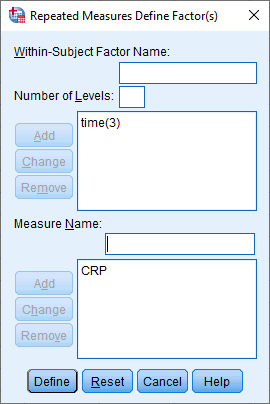
مرحله (4)

بر روی دکمه Define کلیک کنید و مانند شکل زیر با پنجره ی Repeated Measures روبرو خواهید شد:

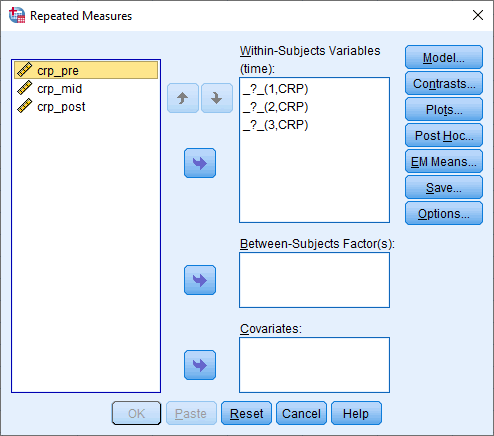
مرحله (5)

crp_pre، crp_mid و crp_post را به ترتیب به متغیرهای _?_(1,CRP)، _?_(2,CRP)، _?_(3,CRP) به Within-Subjects Variables (time) انتقال دهید. در نهایت با صفحه زیر مواجه خواهید شد:

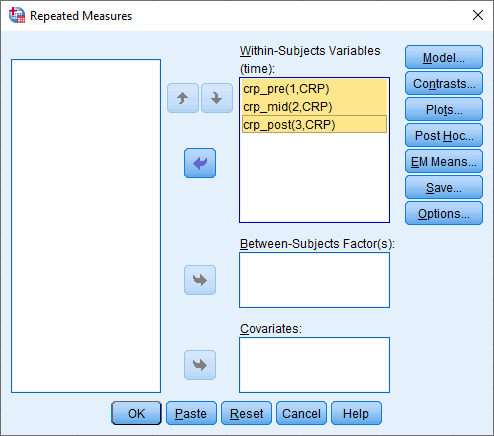
مرحله (6)

روی دکمه Plots کلیک کنید. همانطور که در زیر نشان داده شده است، با پنجره ی Repeated Measures: Profile Plots مواجه خواهید شد:

مرحله (7)

با کلیک بر روی دکمه ، فاکتور درون سوژه ای، time را از کادر Factors به کادر Horizontal Axis منتقل کنید. در نهایت با صفحه زیر مواجه خواهید شد:

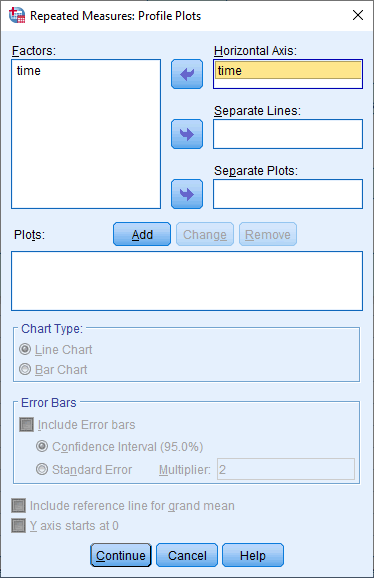
مرحله (8)

بر روی دکمه add کلیک کنید. همانطور که در زیر نشان داده شده است، این کار time را از کادر Horizontal Axis به کادر Plots منتقل می کند:

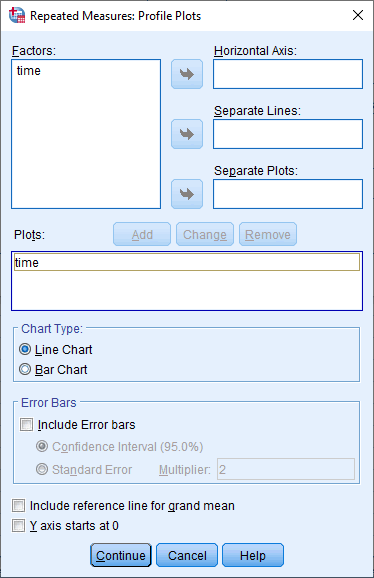
مرحله (9)

بر روی دکمه Continue کلیک کنید و به پنجره ی Repeated Measures باز خواهید گشت.

مرحله (10)

بر روی دکمه EM Means کلیک کنید و مطابق شکل زیر با پنجره ی Repeated Measures: Estimated Margin Means روبرو خواهید شد:

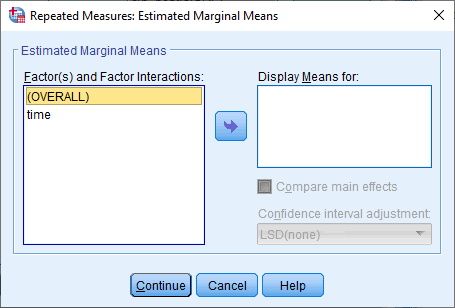
مرحله (11)

با استفاده از دکمه ، time را از کادر Factor(s) and Factor Interactions به کادر Display Means for انتقال دهید. با این کار چک باکس فعال می‌شود (یعنی دیگر خاکستری نمی‌شود). این چک باکس را علامت بزنید و Bonferroni را از منوی تنظیمات Confidence interval adjustment انتخاب کنید. با صفحه زیر روبرو خواهید شد:

مرحله (12)

بر روی دکمه Continue کلیک کنید و به پنجره ی Repeated Measures باز خواهید گشت.

مرحله (13)

بر روی دکمه Options کلیک کنید و مطابق شکل زیر با پنجره ی Repeated Measures: Options روبرو خواهید شد:

مرحله (14)

در ناحیه –Display– چک باکس های Descriptive statistics (آمار توصیفی) و Estimates of effect size (تخمین اندازه اثر) را علامت بزنید. با صفحه زیر روبرو خواهید شد:

مرحله (15)

بر روی دکمه Continue کلیک کنید و به پنجره ی Repeated Measures باز خواهید گشت.

مرحله (16)

بر روی دکمه OK کلیک کنید. با اجرای تمام این مراحل خروجی تولید می شود.

پس از اجرای روش 16 مرحله ای بالا، نتایج یک ANOVA اندازه گیری های مکرر را با یک آزمون تعقیبی (post hoc test) ایجاد خواهید کرد. این خروجی را در ادامه مورد بحث قرار می دهیم. ولی قبل از بررسی خروجی نحوه تست کردن با ورژن 24 و ورژن های قبل از آن SPSS Statistics را نشان میدهیم.

SPSS Statistics ورژن 24 یا ورژن قبلی SPSS Statistics

تمام مراحل تست در این ورژن ها مانند مراحل گفته شده برای ورژن های بالاتر است با این تفاوت که مانند شکل زیر پنجره ی Repeated Measures: Options در مرحله 13 با پنجره اصلی ادغام شده است:

خروجی SPSS Statistics از ANOVA اندازه گیری های مکرر

SPSS Statistics در تجزیه و تحلیل ANOVA اندازه گیری های مکرر خود، جداول زیادی تولید می کند. در این بخش، ما فقط جداول اصلی مورد نیاز برای درک نتایج خود را از ANOVA اندازه گیری های مکرر به شما نشان می دهیم.

جدول عوامل درون سوژه ای (Within-Subjects Factors)

جدول Within-Subjects Factors گروه های متغیر مستقل خود را به ما یادآوری می کند (که در SPSS Statistics ” within-subject factor” نامیده می شود) و نقاط زمانی 1، 2 و 3 را برچسب گذاری می کند. بعداً هنگام تجزیه و تحلیل نتایج در جدول مقایسه های زوجی (Pairwise Comparisons) به این برچسب ها نیاز خواهیم داشت. مراقب باشید که با ستون “Dependent Variable” در این جدول اشتباه نگیرید، زیرا به نظر می رسد که زمان های مختلف، متغیر وابسته ما هستند. در حالی که این درست نیست برچسب ستون به این واقعیت اشاره دارد که متغیر وابسته “CRP” در هر یک از این نقاط زمانی اندازه گیری می شود.

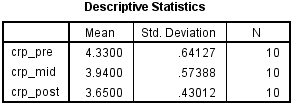
جدول آمار توصیفی (Descriptive Statistics)

جدول Descriptive Statistics به سادگی آمار توصیفی مهمی را برای این تجزیه و تحلیل ارائه می دهد، همانطور که در زیر نشان داده شده است:

جدول آزمون های تأثیرات درون سوژه ای (Tests of Within-Subjects Effects)

جدول Tests of In-Subjects Effects به ما می گوید که آیا به طور کلی تفاوت معنی داری بین میانگین ها در مقاطع زمانی مختلف وجود دارد یا خیر.

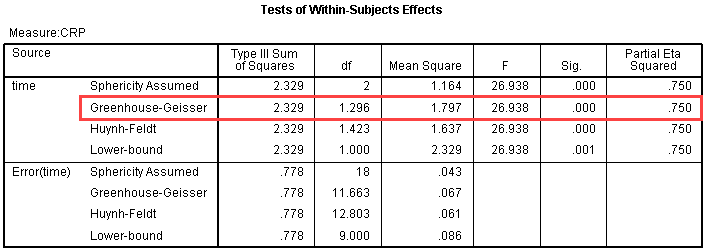
از این جدول می‌توانیم مقدار F را برای عامل “time”، سطح معنی داری مرتبط و اندازه اثر (Partial Eta Squared (مربع اتای جزئی)) کشف کنیم. از آنجایی که داده‌های ما فرض کروی بودن را نقض می‌کنند، به مقادیر موجود در ردیف “Greenhouse-Geisser” نگاه می‌کنیم (همانطور که با رنگ قرمز در تصویر نشان داده شده است). ما می‌توانیم گزارش کنیم که هنگام استفاده از ANOVA با اندازه‌گیری‌های مکرر با تصحیح Greenhouse-Geisser ، میانگین نمرات غلظت CRP از نظر آماری تفاوت معنی‌داری داشت.

F(1.296, 11.663)=26.938,p<.0005

جدول مقایسه های زوجی (Pairwise Comparisons)

نتایج ارائه شده در جدول قبلی به ما اطلاع داد که در مجموع تفاوت معنی داری در میانگین داریم، اما نمی دانیم این تفاوت ها کجا رخ داده است. این جدول نتایج post hoc test (آزمون تعقیبی) Bonferroni را ارائه می‌کند. که به ما امکان می‌دهد بفهمیم کدام ابزارهای خاص متفاوت هستند. به یاد داشته باشید، اگر نتیجه کلی ANOVA شما قابل توجه نباشد، نباید جدول Pairwise Comparisons را بررسی کنید.

با نگاهی به جدول بالا، باید برچسب های مرتبط با نقاط زمانی آزمایش خود را از جدول In-Subject Factors به خاطر بسپاریم. این جدول سطح اهمیت تفاوت بین نقاط زمانی فردی را به ما می دهد. می بینیم که تفاوت آماری معنی داری در غلظت CRP قبل از مداخله در مقایسه با 3 ماه پس از مداخله (0.0005>p) و از قبل از مداخله تا بعد از مداخله (0.001=p) وجود داشت، اما تفاوت معنی داری نداشت. تفاوت از 3 ماه قبل از مداخله در مقایسه با بعد از مداخله (0.054 = p). از ستون “Mean Difference (I-J)” می توانیم ببینیم که غلظت CRP در این نقطه زمانی به طور قابل توجهی کاهش یافته است.

همچنین ممکن است قبل از اینکه به نتایج خود نگاه کنید، بین مقاطع زمانی خاصی که به نظر شما جالب هستند، مقایسه کنید. برای مثال، ممکن است علاقه خود را به دانستن تفاوت غلظت CRP بین نقاط زمانی قبل و بعد از مداخله ابراز کرده باشید. این نوع مقایسه اغلب کنتراست برنامه ریزی شده (planned contrast) یا کنتراست ساده برنامه ریزی شده (planned simple contrast) نامیده می شود. با این حال، لازم نیست خود را به مقایسه بین دو نقطه زمانی محدود کنید. شما ممکن است علاقه مند به درک تفاوت در CRP بین نقطه زمانی قبل از مداخله و میانگین نقاط زمانی اواسط و پس از مداخله بوده باشید. این کنتراست پیچیده (complex contrast) نامیده می شود. همه این نوع کنتراست برنامه ریزی شده در SPSS Statistics موجود است.

نمودار نمایه (Profile Plot)

این نمودار آخرین خروجی این تحلیل است. ما آن را نشان می دهیم تا بتوانید برخی از محدودیت های انجام این کار را در قالب فعلی آن مشاهده کنید. شما می توانید بسیاری از ویژگی های (features/properties) محورهای نمودار را با استفاده از SPSS Statistics تغییر دهید. این کار بسیار مهم است. زیرا این نمودارهای Profile همیشه تمایل دارند با انتخاب محدوده مقادیر محور y که خیلی باریک است، تفاوت های بین میانگین ها را اغراق نمایی کنند. در این مورد، مشخص است که اکثر افراد غلظت CRP از 0 تا 3 دارند، بنابراین باید در نمودار Profile که تولید می کنید = این را در نظر بگیرید. با این حال، این نمودار می تواند در به دست آوردن درک آسان از نتایج جدولی مفید باشد.

گزارش خروجی

ANOVA اندازه گیری های مکرر با تصحیح Greenhouse-Geisser مشخص کرد که میانگین غلظت CRP از نظر آماری بین نقاط زمانی تفاوت معنی داری دارد (F(1.298,11.663)=26.938,P<0.0005). تجزیه و تحلیل Post hoc با تعدیل Bonferroni نشان داد که غلظت CRP از نظر آماری از قبل از مداخله به مدت سه ماه (95% فاصله اطمینان (CI)، 0.24 تا 0.54) میلی‌گرم در لیتر، P <.0005) و از قبل از مداخله به بعد از مداخله (0.68 (95% CI، 0.34 تا 1.02) میلی‌گرم در لیتر، p = 0.001) کاهش یافته است، اما از سه ماه به بعد از مداخله (0.29 (95% CI، 0.01- تا 0.59) میلی‌گرم در لیتر، p = 0.054) کاهش نیافته است.

مطالب زیر را هم از دست ندهید:

آزمون نرمال بودن با استفاده از SPSS Statistics

انواع متغیر و تحقیقات تجربی و غیر تجربی

ANCOVA یک طرفه در SPSS Statistics