
معیارهای گرایش به مرکز (Measures of Central Tendency)
- پری کرمی
- اسفند 27, 1401
- بدون دیدگاه
معیارهای گرایش به مرکز
معرفی
معیار گرایش به مرکز (Measures of Central Tendency) یک مقدار واحد است که تلاش می کند مجموعه ای از داده ها را با شناسایی موقعیت مرکزی در آن مجموعه داده توصیف کند. به این ترتیب، معیارهای گرایش به مرکز گاهی اوقات معیارهای مکان مرکزی (measures of central location) نامیده می شوند. آنها همچنین به عنوان خلاصه آمار طبقه بندی می شوند. متوسط (mean) (اغلب میانگین (average) نامیده می شود) که بیشتر با آن آشنا هستید، نمونه ای از معیار گرایش به مرکز است با این حال موارد دیگری مانند میانه (median) و نما یا مد (mode) وجود دارد.
میانگین، میانه و مد همگی معیارهای معتبری برای گرایش به مرکز هستند، اما در شرایط مختلف، برخی از معیارهای گرایش به مرکز مناسب تر از سایر معیارها هستند. در بخشهای بعدی میانگین، مد و میانه را بررسی میکنیم و نحوه محاسبه آنها و چه شرایطی برای استفاده از آنها مناسبتر است، را بیان می کنیم.
میانگین (حسابی (Arithmetic))
محبوب ترین و شناخته شده ترین معیار گرایش به مرکز است. اگرچه استفاده از آن اغلب برای داده های پیوسته است با این حال می توان آن را برای داده های گسسته نیز استفاده کرد. میانگین برابر است با مجموع تمام مقادیر موجود در مجموعه داده تقسیم بر تعداد مقادیر موجود در مجموعه داده. بنابراین، اگر در یک مجموعه n داده داشته باشیم و آنها دارای مقادیر x1، x2،…، x3 باشند، میانگین نمونه، که معمولا با x̄ نشان داده می شود، این است:
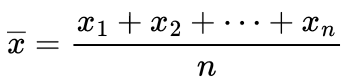
این فرمول معمولاً به روشی کمی متفاوت با استفاده از حرف کاپیتول یونانی ![]() نوشته میشود، که “سیگما” تلفظ میشود، که به معنای “مجموع…” است:
نوشته میشود، که “سیگما” تلفظ میشود، که به معنای “مجموع…” است:

شاید متوجه شده باشید که فرمول بالا به میانگین نمونه اشاره دارد. بنابراین، چرا ما آن را یک میانگین نمونه نامیده ایم؟ به این دلیل که در آمار، نمونه ها و جمعیت ها معانی بسیار متفاوتی دارند و این تفاوت ها بسیار مهم است، حتی اگر در مورد میانگین، به یک صورت محاسبه شود. برای تأیید اینکه ما در حال محاسبه میانگین جامعه هستیم و نه میانگین نمونه، از حرف کوچک یونانی “mu” استفاده می کنیم که به صورت µ نشان داده می شود:
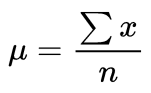
میانگین اساساً مدلی از مجموعه داده های شما است. این مقداری است که رایج ترین است. با این حال، اغلب میانگین یکی از مقادیر واقعی موجود در مجموعه داده های شما نیست. با این حال، یکی از ویژگی های مهم آن این است که خطا را در پیش بینی هر یک از مقادیر در مجموعه داده شما به حداقل می رساند. یعنی مقداری است که کمترین مقدار خطا را از سایر مقادیر موجود در مجموعه داده ایجاد می کند.
یک ویژگی مهم میانگین این است که به عنوان بخشی از محاسبه، هر مقدار در مجموعه داده شما شامل را می شود. علاوه بر این، میانگین تنها معیار گرایش به مرکز است که در آن مجموع انحرافات هر مقدار از میانگین همیشه صفر است.
چه زمانی نباید از میانگین استفاده کنید
میانگین یک نقطه ضعف اصلی دارد. آن هم این است که در معرض تأثیر داده های پرت (outliers) است. داده های پرت مقادیری هستند که در مقایسه با بقیه مجموعه داده ها به دلیل کوچک یا بزرگ بودن مقدار، غیرعادی هستند. به عنوان مثال، دستمزد کارکنان یک کارخانه را در زیر در نظر بگیرید:
| کارکنان | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| حقوق (میلیون تومان) |
1.5 | 1.8 | 1.6 | 1.4 | 1.5 | 1.5 | 1.2 | 1.7 | 9 | 9.5 |
میانگین حقوق برای این ده کارمند 3.07 میلیون تومان است. با این حال، بررسی دادههای خام نشان میدهد که این مقدار متوسط ممکن است بهترین راه برای منعکس کردن دقیق حقوق معمولی یک کارگر نباشد، زیرا اکثر کارگران حقوقی در محدوده 1.2 تا 1.8 میلیون تومان دارند. میانگین با دو حقوق کلان (9 و 9.5) منحرف می شود. بنابراین، در این شرایط، مایلیم معیار بهتری از گرایش به مرکز داشته باشیم. همانطور که بعداً متوجه خواهیم شد، گرفتن میانه معیار بهتری برای سنجش گرایش به مرکز در این وضعیت خواهد بود.
زمان دیگری که معمولاً میانه را بر میانگین (یا مد) ترجیح میدهیم، زمانی است که دادههای ما چوله ای است (یعنی توزیع فرکانس برای دادههای ما انحراف دارد). زمانی که توزیع داده ها کاملا نرمال هستند، میانگین، میانه و مد یکسان هستند. علاوه بر این، همه آنها معمولی ترین مقدار را در مجموعه داده ها نشان می دهند. با این حال، وقتی دادهها منحرف میشوند، میانگین توانایی خود را برای ارائه بهترین مکان مرکزی برای دادهها از دست میدهد، زیرا دادههای منحرف شده آن را از مقدار معمولی دور میکند. با این حال، میانه به بهترین وجه این موقعیت را حفظ می کند و به شدت تحت تأثیر مقادیر منحرف نیست. در بخش های بعدی، این بحث با جزئیات بیشتری توضیح داده شده است.
میانه
میانه مقدار میانی برای مجموعه ای از داده ها است که به ترتیب از کوچک به بزرگ یا بلعکس مرتب شده اند. میانه، کمتر تحت تأثیر داده های پرت و ناهموار قرار می گیرد. برای محاسبه میانه، فرض کنید داده های زیر را داریم:

ابتدا باید آن داده ها را به ترتیب بزرگی مرتب کنیم:

در این مجموعه که 11 داده وجود دارد، داده ی وسط (56) به عنوان میانه در نظر گرفته می شود. وقتی تعداد داده ها “فرد” باشد این کار به راحتی انجام می شود. اما وقتی تعداد داده ها “زوج” باشد (مثلا 10 تا)، شما باید دو داده وسط را در نظر بگیرید و میانگین آن دو را به عنوان میانه در نظربگیرید. بنابراین، اگر به مثال زیر نگاه کنیم:

ما دوباره آن داده ها را به ترتیب بزرگی مرتب می کنیم:

دو داده وسط (55 و56) را در مجموعه داده های خود در نظر بگیرید و میانگین آنها 55.5 به دست می آید که به عنوان میانه در نظر گرفته می شود.
مد
مد بیشترین مقدار در مجموعه داده ما است. در یک نمودار میله ای، بالاترین میله در نمودار نشان دهنده ی مد است. بنابراین، گاهی اوقات می توانید مد را به عنوان محبوب ترین گزینه در نظر بگیرید. نمونه ای از یک مد در زیر ارائه شده است:
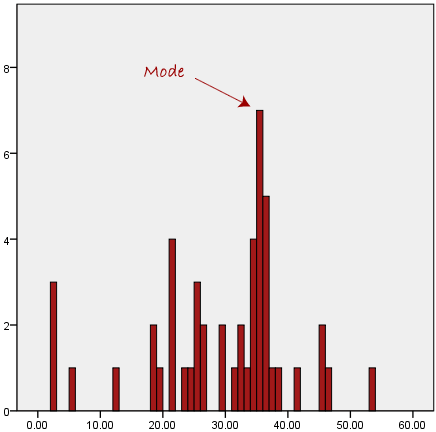
به طور معمول، مد برای داده های طبقه ای (categorical data) استفاده می شود که مایلیم بدانیم کدام طبقه یا دسته رایج ترین است، همانطور که در زیر نشان داده شده است:
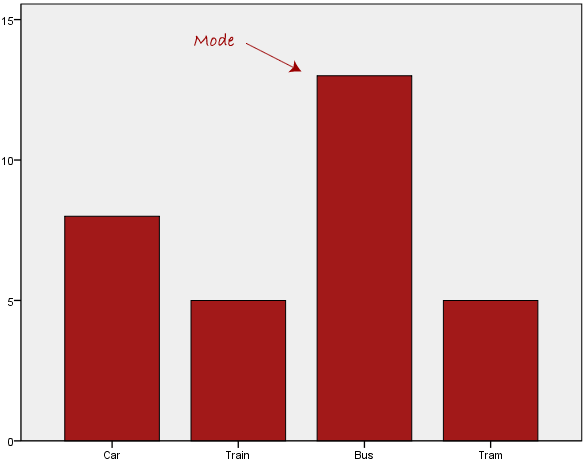
در بالا می بینیم که رایج ترین شکل حمل و نقل، در این مجموعه داده، اتوبوس است. با این حال، یکی از مشکلات مد این است که منحصر به فرد نیست، بنابراین زمانی که دو یا چند مقدار داشته باشیم که بالاترین فرکانس را به اشتراک می گذارند، ما را با مشکلی مانند زیر مواجه می کند:
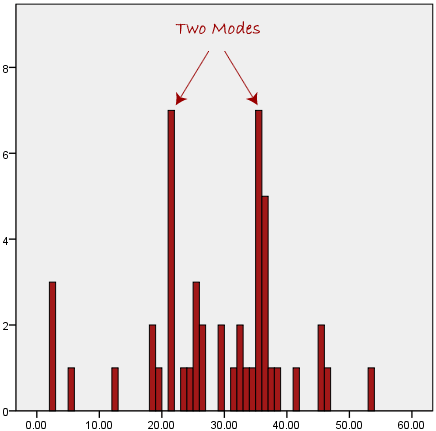
ما اکنون درگیر این هستیم که کدام مد به بهترین وجه گرایش به مرکز داده ها را توصیف می کند. این به ویژه زمانی مشکل ساز است که داده های پیوسته داشته باشیم، زیرا احتمال بیشتری وجود دارد که هیچ مقدار متداول تر از دیگری نداشته باشیم. به عنوان مثال، اندازه گیری وزن 30 نفر (با دقت 0.1 کیلوگرم) را در نظر بگیرید. چقدر احتمال دارد که دو یا چند نفر با وزن دقیقاً یکسان (مثلاً 67.4 کیلوگرم) پیدا کنیم؟ پاسخ، احتمالاً بسیار بعید است. وزن بسیاری از افراد ممکن است به این مقدار نزدیک باشند، اما با چنین نمونه کوچک (30 نفره) و طیف وسیعی از وزنهای احتمالی، بعید است که دو نفر با وزن دقیقاً یکسان را پیدا کنید. به همین دلیل است که این مد به ندرت با داده های پیوسته استفاده می شود.
همانطور که در نمودار زیر نشان داده شده است، مشکل دیگر مد این است که وقتی رایجترین داده از بقیه دادههای مجموعه داده دور است، معیار بسیار خوبی از گرایش به مرکز به ما ارائه نمیدهد:
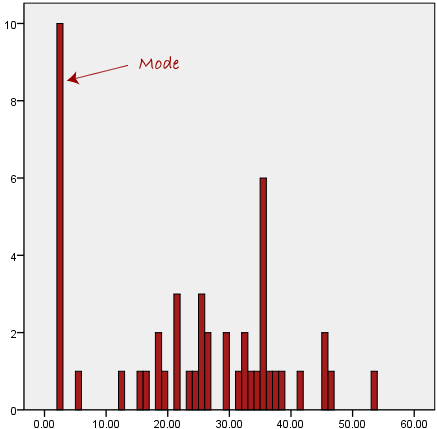
در نمودار بالا، مد دارای مقدار 2 است. با این حال، ما به وضوح میتوانیم ببینیم که این مد نماینده دادهها نیست، که بیشتر در محدوده 20 تا 30 متمرکز شدهاند. استفاده از مد برای توصیف گرایش به مرکز این مجموعه داده گمراه کننده خواهد بود.
توزیع های چوله ای (Skewed Distributions) و میانگین و میانه
ما اغلب بررسی میکنیم که آیا دادههای ما به طور نرمال توزیع شدهاند یا نه؟ زیرا این یک فرض رایج است که زیربنای بسیاری از آزمایشهای آماری است. نمونه ای از یک مجموعه داده با توزیع نرمال در زیر ارائه شده است:
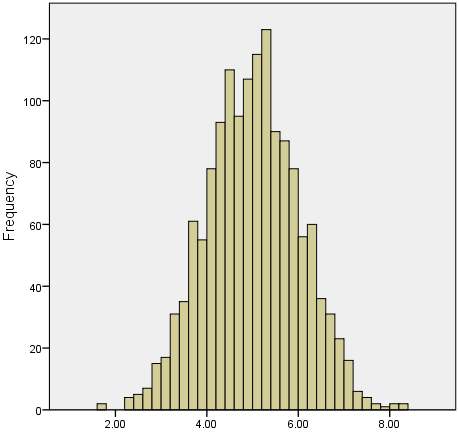
هنگامی که یک نمونه با توزیع نرمال دارید، می توانید به طور قانونی از میانگین یا میانه به عنوان معیار گرایش به مرکز خود استفاده کنید. در واقع، در هر توزیع متقارن، میانگین، میانه و مد برابر هستند. با این حال، در این وضعیت، میانگین به طور گسترده ای به عنوان بهترین معیار گرایش به مرکز ترجیح داده می شود، زیرا این معیار است که تمام مقادیر موجود در مجموعه داده برای محاسبه آن را شامل می شود و هر تغییری در هر یک از مقادیر، بر مقدار آن تأثیر می گذارد. این مسئله در مورد میانه یا مد صدق نمی کند.
با این حال، زمانی که دادههای ما توزیع نرمال نداشته و دارای انحراف هستند (توزیع چوله ای)، مانند مجموعه دادههای زیر، متوجه میشویم که میانگین به سمت انحراف کشیده میشود.

در این شرایط، میانه به طور کلی بهترین نماینده مکان مرکزی داده ها در نظر گرفته می شود. هرچه توزیع چوله ای بیشتر باشد، تفاوت بین میانه و میانگین بیشتر است و باید بر استفاده از میانه در مقابل میانگین تاکید بیشتری شود. یک مثال کلاسیک از توزیع ناهنجار بالایی از درآمد (حقوق) است، که در آن با وجود افراد با درآمد خیلی بالاتر اگر به جای میانه، میانگین بیان شوند و نمایش نادرستی از درآمد معمولی ارائه می دهند.
اگر تست های نرمال بودن نشان دهند که داده ها غیرنرمال هستند، مرسوم است که به جای میانگین از میانه استفاده شود. با این حال، این بیشتر یک قانون سرانگشتی است تا یک دستورالعمل دقیق. گاهی اوقات، اگر میانه و میانگین تفاوت قابل ملاحظه ای نداشته باشند (ارزیابی ذهنی)، و اگر امکان مقایسه آسان تر با تحقیقات قبلی را فراهم کند، محققان تمایل دارند میانگین توزیع چوله ای را گزارش کنند.
خلاصه زمان استفاده از میانگین، میانه و مد
لطفاً از جدول خلاصه زیر استفاده کنید تا بدانید بهترین معیار گرایش به مرکز با توجه به انواع مختلف متغیرها چیست.
| نوع متغیر | بهترین معیار گرایش به مرکز |
| اسمی (Nominal) | مد |
| ترتیبی (Ordinal) | میانه |
| فاصله ای (Interval) / نسبتی (Rati) (غیر چوله ای) | میانگین |
| فاصله ای (Interval) / نسبتی (Rati) (چوله ای) | میانه |
سوالات متداول – معیارهای گرایش به مرکز
لطفاً در زیر پاسخ چند سؤال متداول که در مورد معیارهای گرایش به مرکز پرسیده می شود، را ببینید.
بهترین معیار برای سنجش گرایش به مرکز چیست؟
با توجه به دادههایی که تحلیل میکنید، اغلب میتوان یک “بهترین” معیار برای گرایش به مرکز وجود داشته باشد، اما “بهترین” معیار برای گرایش به مرکز وجود ندارد. این به این دلیل است که استفاده از میانه، میانگین یا مد به نوع داده ای که دارید بستگی دارد (مانند داده های اسمی یا پیوسته) و ممکن است داده های شما دارای داده های پرت و یا انحراف از حالت نرمال هستند.
در یک توزیع به شدت چوله ای، بهترین شاخص گرایش به مرکز چیست؟
معمولاً استفاده از میانگین در چنین شرایطی که داده های شما دارای انحراف است، نامناسب است. شما معمولاً میانه یا مد را انتخاب می کنید که معمولاً میانه ترجیح داده می شود.
آیا همه داده ها میانه، مد و میانگین دارند؟
هم بله و هم خیر!!!. همه داده های پیوسته دارای میانه، مد و میانگین هستند. به طور دقیق، داده های ترتیبی فقط یک میانه و مد دارند و داده های اسمی فقط یک مد دارند. با این حال، در مورد اینکه آیا میانگین را می توان با داده های ترتیبی استفاده کرد یا خیر، بین آماردان ها اتفاق نظر حاصل نشده است، و اغلب می توانید میانگین گزارش شده برای داده های لیکرت (Likert data) را در تحقیقات مشاهده کنید. نمونه ای از داده های لیکریت در زیر آمده است:

چه زمانی میانگین بهترین معیار گرایش به مرکز است؟
زمانی که توزیع داده شما پیوسته و متقارن است توزیع نرمال دارند، میانگین معمولاً بهترین معیار گرایش به مرکز است. مانند زمانی که داده های شما به طور می شوند، استفاده می شود. با این حال، همه چیز به آنچه می خواهید از داده های خود نشان دهید بستگی دارد.
چه زمانی مد بهترین معیار برای سنجش گرایش به مرکز است؟
این مد کمترین استفاده را در بین معیارهای گرایش به مرکز دارد و فقط در هنگام برخورد با دادههای اسمی قابل استفاده است. به همین دلیل، هنگام برخورد با داده های اسمی مد بهترین معیار برای سنجش گرایش به مرکز خواهد بود (زیرا تنها مورد مناسب برای استفاده است). میانگین و/ یا میانه معمولاً هنگام برخورد با انواع دیگر داده ها ترجیح داده می شود، اما این بدان معنا نیست که هرگز با این نوع داده ها استفاده نمی شود.
چه زمانی میانه بهترین معیار برای سنجش گرایش به مرکز است؟
وقتی مجموعه دادههای شما چوله ای است (به عنوان مثال، یک توزیع چوله ای را تشکیل میدهد) یا با دادههای ترتیبی سروکار دارید، میانه معمولاً به سایر معیارهای گرایش به مرکز ترجیح داده میشود. با این حال، مد نیز می تواند در این شرایط مناسب باشد، اما معمولا استفاده نمی شود.
زمانی که داده ها دارای مقادیر پرت هستند، مناسب ترین معیار برای سنجش گرایش به مرکز چیست؟
میانه معمولاً در این موقعیت ها ترجیح داده می شود. زیرا مقدار میانگین می تواند توسط مقادیر پرت تحت تاثیر قرار گیرند. با این حال، این بستگی به میزان تأثیرگذاری نقاط پرت دارد. اگر آنها میانگین را به طور قابل توجهی تحریف نکنند، معمولاً استفاده از میانگین به عنوان معیار گرایش به مرکز ترجیح داده می شود.
در یک مجموعه داده به طور کاملا نرمال توزیع شده، کدام بزرگتر است: مد، میانه یا میانگین؟
اگر مجموعه داده کاملاً نرمال باشد، میانگین، میانه و میانگین با یکدیگر برابر هستند (یعنی یک مقدار).
برای هر مجموعه داده، کدام معیارهای گرایش به مرکز فقط یک مقدار دارند؟
میانه و میانگین فقط می توانند یک مقدار برای یک مجموعه داده معین داشته باشند ولی مد می تواند بیش از یک مقدار داشته باشد.
مطالب زیر را هم از دست ندهید:
ضریب همبستگی رتبهای اسپیرمن (Spearman rank-order correlation coefficient) با استفاده از SPSS
آزمون H کروسکال-والیس (H Kruskal-Wallis) با استفاده از Stata
MANOVA یک طرفه با استفاده از Stata
رسم نمودار پراکندگی (نقطه ای) (Scatterplot) با استفاده از SPSS
ایجاد نمودار میله ای خوشه ای (Clustered Bar Chart) با استفاده از SPSS
ANCOVA یک طرفه در SPSS Statistics
ANOVA اندازه گیری های مکرر دو طرفه با استفاده از SPSS Statistics
ANOVA با اندازه گیری های مکرر با استفاده از SPSS Statistics
ANOVA دو طرفه در SPSS Statistics
ANOVA مخلوط با استفاده از SPSS Statistics
انواع متغیر و تحقیقات تجربی و غیر تجربی
ایجاد متغیر های ساختگی در SPSS
آزمون Jonckheere-Terpstra (جانكهير ترپسترا) با استفاده از SPSS
آزمون Q کوکران (Cochran’s Q) با استفاده از SPSS
آزمون t نمونه تکی با استفاده از SPSS Statistics
آزمون t وابسته با استفاده از SPSS
آزمون t وابسته برای نمونه های جفت شده
آزمون رتبه علامتدار ویلکاکسون (Wilcoxon signed-rank test) با استفاده از SPSS
آزمون مربع کای (Chi-Square) با استفاده از SPSS
آزمون مک نمار (McNemar’s test) با استفاده از SPSS
آزمون نرمال بودن با استفاده از SPSS Statistics
آزمون یو من ویتنی (Mann-Whitney U) با استفاده از SPSS
آمار توصیفی (descriptive) و استنباطی (inferential)
آنالیز اجزای اصلی (PCA) با استفاده از SPSS
تعدیل کننده دو وضعیتی (Dichotomous Moderator) با استفاده از SPSS
دی سامرز (Somers’ d) با استفاده از SPSS
رگرسیون پواسون با استفاده از SPSS
رگرسیون چندگانه با استفاده از SPSS
رگرسیون خطی با استفاده از SPSS
رگرسیون لجستیک ترتیبی با استفاده از SPSS
رگرسیون لجستیک چند جمله ای در SPSS
رگرسیون لجستیک دو جمله ای با استفاده از SPSS
ضریب همبستگی تاوی- بی کندال (Kendall’s Tau-b correlation coefficient) با استفاده از SPSS
گامای گودمن و کروسکال (Goodman and Kruskal’s gamma) با استفاده از SPSS

