آزمون t زوجی و یا جفت شده (paired t-test) با استفاده از Minitab

پری کرمی
مارس 10, 2023
بدون دیدگاه

آزمون t زوجی و یا جفت شده با استفاده از Minitab

مقدمه

آزمون t زوجی و یا جفت شده (paired t-test) برای تعیین وجود تفاوت آماری معنی داری در میانگین متغیر وابسته بین دو گروه مرتبط استفاده می شود. این آزمون همچنین به عنوان آزمون t نمونه زوجی (paired-samples t-test) و یا آزمون t وابسته (dependent t-test) نیز شناخته می شود.

برای مثال، می‌توانید از آزمون t زوجی استفاده کنید تا بفهمید آیا تفاوتی در اضطراب امتحان دانش‌آموزان قبل و بعد از انجام یک برنامه هیپنوتیزم درمانی که برای کاهش استرس طراحی شده وجود دارد یا خیر. در این مثال متغیر وابسته «اضطراب امتحان» خواهد بود و دو گروه مرتبط، دو «نقطه زمانی» یعنی اضطراب امتحان «قبل» و «بعد از» تحت برنامه هیپنوتیزم درمانی متفاوت خواهند بود.

در این آموزش، ما به شما نشان می دهیم که چگونه با استفاده از Minitab یک آزمون t زوجی را انجام دهید، همچنین نتایج این آزمون را تفسیر و گزارش کنید. با این حال، قبل از اینکه شما را با این روش آشنا کنیم، باید فرضیات مختلفی را که داده‌های شما باید رعایت کنند تا یک آزمون t زوجی به شما یک نتیجه معتبر بدهد، بدانید. در ادامه به این فرضیات می پردازیم.

فرضیات

آزمون t زوجی دارای چهار “فرض” است. شما نمی توانید دو فرض اول را با Minitab بررسی کنید زیرا به طراحی مطالعه شما و انتخاب متغیرها مربوط می شود. با این حال، باید بررسی کنید که آیا مطالعه شما با این دو فرض مطابقت دارد یا خیر. اگر این فرضیات برآورده نشوند، باید به جای آزمون t زوجی از آزمون آماری دیگری استفاده کنید. فرضیات #1 و #2 در زیر توضیح داده شده است:

فرض شماره 1:

متغیر وابسته شما باید در سطح پیوسته یعنی در مقیاس فاصله ای (interval) یا نسبتی (ratio) اندازه گیری شود. نمونه‌هایی از این متغیرهای پیوسته عبارتند از: ارتفاع، دما، زمان، حقوق، هوش، سن نمره امتحان و غیره می باشد.

فرض شماره 2:

متغیر مستقل شما باید از دو دسته بندی (categorical)، “گروه های مرتبط” (related groups) یا “جفت همسان” (matched pairs) تشکیل شده باشد. “گروه های مرتبط” نشان می دهد که شرکت کنندگان یکسان در هر دو گروه حضور دارند. دلیل وجود شرکت‌کنندگان یکسان در هر گروه این است که هر سوژه در دو نوبت بر روی یک متغیر وابسته اندازه‌گیری شده است. همچنین برای گروه‌های مرتبط رایج است که دو شرایط متفاوتی را که همه شرکت‌کنندگان تحت آن قرار می‌گیرند منعکس کنند این شرایط گاهی اوقات مداخله (interventions)، درمان (treatments) یا آزمایش (trials) نامیده می‌شوند.

فرضیات شماره 3 و 4 مربوط به ماهیت داده های شما هستند و می توان آنها را با استفاده از Minitab بررسی کرد. باید این فرضیات بررسی کنید. در غیر این صورت، نتایجی که هنگام اجرای یک آزمون t زوج به دست می‌آورید ممکن است معتبر نباشند.

فرض شماره 3:

در تفاوت بین دو گروه مرتبط نباید نقاط پرت (outliers) قابل توجهی وجود داشته باشد. نقطه پرت یک داده در مجموعه داده های شما است که از الگوی معمول پیروی نمی کند. نقاط پرت می توانند تأثیر منفی نامتناسبی بر آزمون t زوجی داشته باشند و تفاوت بین دو گروه مرتبط (اعم از افزایش یا کاهش مقادیر متغیر وابسته) را مخدوش کنند، که دقت آزمون را کاهش می دهد. همچنین آنها می توانند بر اهمیت آماری آزمون تأثیر بگذارند. خوشبختانه، هنگام استفاده از Minitab برای اجرای یک آزمون t زوجی روی داده‌های خود، می‌توانید به راحتی نقاط پرت احتمالی را تشخیص دهید.

فرض شماره 4:

تفاوت های متغیر وابسته بین دو گروه مرتبط باید تقریباً به طور نرمال توزیع شود. ما در مورد آزمون t زوجی صحبت می‌کنیم که فقط به داده‌های تقریباً نرمال نیاز دارد. به این معنی که این فرض می‌تواند کمی نقض شود و همچنان نتایج معتبری ارائه شود. شما می توانید با استفاده از آزمون Shapiro-Wilk نرمال بودن (یا نرمالیته) را بررسی کنید. اگر مقادیر تفاوت به طور معمول توزیع شده ندارید، بهتر است به جای آزمون t زوجی، رتبه علامت‌دار ویلکاکسون (Wilcoxon signed-rank test) را اجرا کنید.

در عمل، بررسی این فرضیات احتمالاً بیشتر وقت شما را هنگام انجام یک آزمون t زوجی می‌گیرد. با این حال، کار سختی نیست و Minitab تمام ابزارهایی را که برای انجام این کار نیاز دارید در اختیار شما قرار می دهد.

در بخش بعدي روش Minitab مورد نیاز برای انجام یک آزمون t زوجی را با فرض اینکه هیچ فرضی نقض نشده است، نشان می‌دهیم. ابتدا، مثالی که برای توضیح روش آزمون t زوجی در Minitab استفاده كرده ايم، را ارائه می‌کنیم.

مثال

محققی می‌خواهد تعیین کند که آیا یک برنامه هیپنوتیزم درمانی می‌تواند به کاهش مصرف سیگار در میان سیگاری‌های طولانی مدت (افرادی که بیش از 10 سال است که به طور منظم سیگار می‌کشند) کمک کند يا نه؟. بنابراین، متغیر وابسته «مصرف سیگار» مي باشد که بر حسب میانگین تعداد سیگار مصرف شده اندازه‌گیری شد و متغیر مستقل «زمان» است که شامل دو گروه مرتبط «قبل» و «بعد» از برنامه هیپنوتیزم درمانی مي باشد.

برای انجام این بررسی، محقق 20 سیگاری طولانی مدت را انتخاب کرد. همه این 20 شرکت کننده در این مداخله شرکت کردند که یک برنامه هیپنوتیزم درمانی 6 هفته ای که برای کمک به ترک سیگار طراحی شده بود، بر روي آنها اجرا شد. میزان مصرف سیگار شرکت کنندگان ابتدا «قبل از مداخله» و سپس برای بار دوم «بعد از» مداخله ثبت شد. این معمولاً به عنوان طرح مطالعه “پیش آزمون پس آزمون” (pre-test post-test)‌ شناخته می شود.

برای تعیین اینکه آیا تفاوت معنی داری در مصرف سیگار قبل و بعد از برنامه هیپنوتیزم درمانی وجود دارد یا خیر، از آزمون t زوجی استفاده شد.

تنظیمات در Minitab

در Minitab، دو گروه مرتبط را طوری تنظیم کردیم که انگار دو متغیر هستند. بنابراین در زیر ستون C1 نام اولین گروه مرتبط یعنی Pre را وارد کردیم. سپس در زیر ستون C2 نام دومین گروه مرتبط یعنی Post را وارد کردیم. در نهایت، مقادیر متغیر وابسته را برای هر یک از دو گروه مرتبط یعنی مصرف سیگار برای هر شرکت کننده قبل از برنامه هیپنوتیزم درمانی در ستون Pre و مصرف سیگار برای همان شرکت کنندگان بعد از برنامه هیپنوتیزم درمانی در ستون Post وارد کردیم. این مراحل در زیر نشان داده شده است:

مراحل آزمون در Minitab

در این بخش، به شما نشان می‌دهیم که چگونه با استفاده از آزمون t زوجی در Minitab داده‌های خود را تجزیه و تحلیل کنید. البته به شرطی که چهار فرض تعیین شده در بخش فرضیات نقض نشده‌ باشند. بنابراین، سه مرحله مورد نیاز برای اجرای یک آزمون t زوجی در Minitab در زیر نشان داده شده است:

مرحله (1)

همانطور که در زیر نشان داده شده است، روی

Stat > Basic Statistics > Paired t…

در منوی اصلی کلیک کنید:

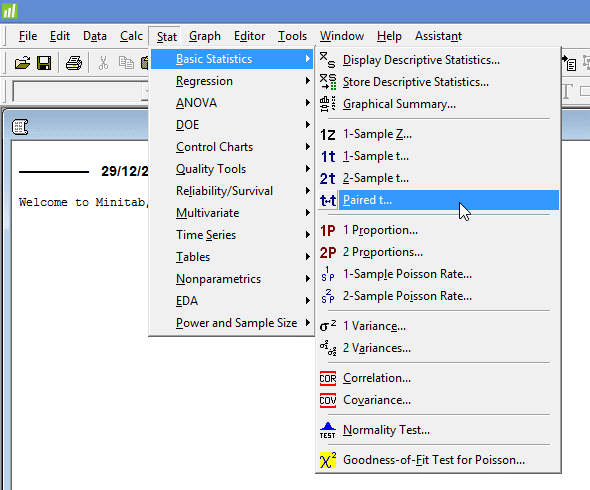
پنجره ی Paired t (Test and Confidence Interval) زیر به شما نمایش داده می شود:

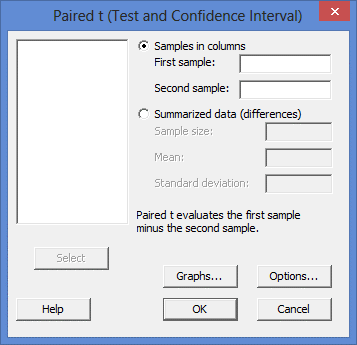
مرحله (2)

گزینه Samples in columns را انتخاب کنید. سپس، یک گروه مرتبط، Post را در کادر First sample و گروه مرتبط دیگر، Pre را در کادر Second sample وارد کنید. در نهایت با پنجره ی زیر روبرو خواهید شد:

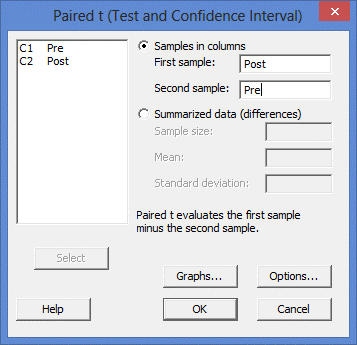
نکته 1: برای انتقال متغیرهای خود، ابتدا باید روی کادر First sample: کلیک کنید تا دو گروه مرتبط شما در کادر سمت چپ اصلی ظاهر شوند (به عنوان مثال، C1 Pre و C2 Post). برای انتقال اولین گروه مرتبط، متغیر مورد نظر را در کادر اصلی سمت چپ انتخاب کنید و دکمه Select را فشار دهید.

توضیح: باید مطمئن شوید که گروه‌های مرتبط خود را در کادرهای صحیح وارد کرده‌اید (یعنی کادرهای First sample و Second sample). چون که در Minitab، همانطور که در مستطیل قرمز رنگ زیر مشخص شده است، تنظیمات به گونه‌ای است که ” t زوجی، اولین نمونه را منهای نمونه دوم ارزیابی می‌کند (Paired t evaluates the first sample minus the second sample):

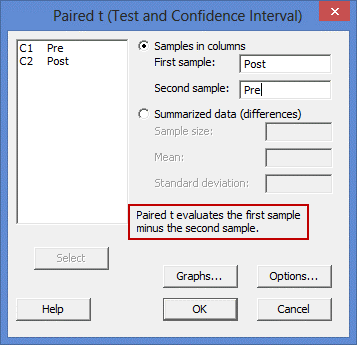
بنابراین، اگر دو گروه مرتبط شما دو «نقطه زمانی» باشند (به عنوان مثال، طرح مطالعه پیش آزمون پس آزمون (pre-test post-test))، (مانند مثال ما در مورد مصرف سیگار قبل و بعد از یک برنامه هیپنوتیزم درمانی)، معمولاً مقادیر مربوط به وابسته را کم می کنید. یعنی مقادیر “قبل از” انجام مداخله از مقادیر “بعد از” مداخله کسر می شود. در چنین حالتی، نقطه زمانی “دوم” به عنوان نمونه اول عمل می کند: و نقطه زمانی “اول” به عنوان نمونه دوم عمل می کند.

متناوباً، اگر طرح مطالعه‌ای دارید که در آن به تفاوت‌های بین دو «شرط» علاقه‌مند هستید (فرض شماره 2)، اغلب یک گروه کنترل (control) و گروه آزمایشی (experimental) وجود خواهد داشت. در چنین حالتی، معمولاً مقادیر متغیر وابسته گروه کنترل را از گروه آزمایشی خود کم می کنید (یعنی گروه آزمایشی منهای گروه کنترل). در چنین حالتی، “گروه آزمایشی” به عنوان نمونه اول عمل می کند: و “گروه کنترل” به عنوان نمونه دوم.

نکته 2: به طور پیش فرض، Minitab از فاصله اطمینان (confidence intervals) 95% استفاده می کند که معادل اعلام اهمیت آماری در سطح p<.05 است. اگر می‌خواهید این مورد را تغییر دهید، می‌توانید ابتدا روی دکمه Options کلیک کنید. همانطور که در زیر نشان داده شده است، پنجره ی Paired t – Options باز می شود:

برای تغییر مقدار فاصله اطمینان، کافی است روی کادر Confidence level: کلیک کنید – که در بالا با رنگ قرمز مشخص شده است – و مقدار را تغییر دهید (به عنوان مثال، مقدار 99.0 معادل اعلام اهمیت آماری در سطح p < 0.01 است).

مرحله (3)

بر روی دکمه OK کلیک کنید تا خروجی Minitab تولید گردد.

تفسیر خروجی آزمون t زوجی در Minitab

خروجی Minitab برای آزمون t زوجی در زیر نشان داده شده است. این خروجی آمار توصیفی مفیدی را برای دو گروه مرتبط که با هم مقایسه شدند، شامل حجم نمونه، میانگین، انحراف معیار و خطای استاندارد میانگین و همچنین نتایج واقعی از آزمون t زوجی ارائه می‌دهد.

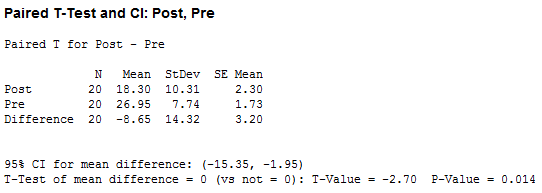
با نگاهی به ستون “Mean”، می بینید که مصرف سیگار در میان شرکت کنندگان پس از برنامه هیپنوتیزم درمانی (18.30 نخ سیگار در ردیف Post) در مقایسه با قبل از برنامه هیپنوتیزم درمانی (26.95 سیگار در ردیف Pre) کمتر بود، با میانگین تفاوت بین دو دوره زمانی 8.65- سیگار (در ردیف Difference نشان داده شده است). همچنین، هنگام مقایسه دو دوره زمانی در ردیف Difference، می‌توانیم ببینیم که انحراف استاندارد 14.32 سیگار (ستون “StDev”) با خطای استاندارد میانگین 3.20 سیگار (ستون “SE Mean”) بود. علاوه بر این، 95% فاصله اطمینان (CI) برای ردیف mean difference، فاصله اطمینان 95% (95% CI) را برای اختلاف میانگین 15.35- تا 1.95- سیگار نشان می دهد.

در سطر پایانی خروجی Minitab، مقدار t بدست آمده (T-Value) برابر 2.70- و اهمیت آماری (2-tailed p-value) آزمون t زوجی (P-Value) با مقدار 0.014 به شما ارائه می شود. از آنجایی که مقدار p کمتر از 0.05 است، می توان نتیجه گرفت که بین دو مقطع زمانی (پیش و پس از آن) تفاوت آماری معنی داری وجود دارد. به عبارت دیگر، تفاوت بین میانگین مصرف سیگار قبل و بعد از برنامه هیپنوتیزم درمانی برابر با صفر نیست. Minitab درجات آزادی را شامل نمی شود، اما درجه آزادی به سادگی اندازه نمونه (ستون “N”) منهای 1 (یعنی N – 1) ) می باشد. بنابراین، در مثال ما درجات آزادی 20 منهای 1 است که 19 می شود.

توجه: علاوه بر خروجی آزمون t زوجی در بالا، شما همچنین باید (الف) نمودارهای جعبه ای (boxplots) که در Minitab ایجاد کرده اید را برای بررسی نقاط پرت، تفسیر کنید (ب) خروجی Minitab تولید شده را برای نرمال بودن Shapiro-Wilk بررسی کنید. به یاد داشته باشید که اگر داده‌های شما با هر یک از این فرضیات گفته شده در بالا مواجه نشدند، خروجی‌ای که از روش آزمون t زوج به دست می‌آورید ممکن است معتبر نباشد و باید اقداماتی را برای مقابله با چنین تخلفاتی انجام دهید (مثلاً، تبدیل داده ها (transforming) با استفاده از Minitab یا استفاده از یک آزمون آماری دیگر).

گزارش خروجی آزمون t زوجی

هنگامی که خروجی آزمون t زوجی خود را گزارش می کنید، بهتر است که شامل موارد زیر باشد:

الف. مقدمه ای بر آنالیزی که انجام دادید.

ب. اطلاعات مربوط به نمونه شما، از جمله تعداد شرکت‌کنندگان در هر گروه از دو گروه مرتبط شما (نکته، اگر اندازه‌های گروه نابرابر بودند یا مقادیر گم شده بودند، باید به آنها هم اشاره کنید).

ج. توضیحی مبنی بر وجود تفاوت معنی دار آماری بین دو گروه مرتبط شما، از جمله میانگین مربوطه (Mean) و انحرافات استاندارد (StDev)، تفاوت میانگین (Difference)، فاصله اطمینان 95 درصد برای تفاوت میانگین (95% CI for mean difference)، مقدار تی (T-Value)، درجات آزادی، و سطح معنی داری، یا به طور خاص تر(P-Value).

بر اساس خروجی Minitab در بالا، می‌توانیم نتایج این مطالعه را به شرح زیر گزارش کنیم:

یک آزمون t زوجی بر روی نمونه ای از 20 سیگاری طولانی مدت اجرا شد تا مشخص شود که آیا تفاوت معنی داری در مصرف سیگار قبل و بعد از یک برنامه هیپنوتیزم درمانی وجود دارد یا خیر. مصرف سیگار شرکت کنندگان بعد از برنامه هیپنوتیزم درمانی (31/10 ± 30/18 نخ سیگار) نسبت به قبل از برنامه هیپنوتیزم درمانی (74/7 ± 95/26 سیگار) کمتر بود. میانگین کاهش معنی‌دار آماری 8.65 سیگار (95% فاصله اطمینان (CI)، 15.35- تا 1.95-).

t(19)=-2.70 , p<.014

برای اینکه درک نتایج خود را برای دیگران راحت‌تر کنید، می‌توانید نمودار میله‌ای (bar chart) با میله‌های خطا (error bars) تولید کنید. جایی که میله‌های خطا می‌تواند انحراف استاندارد، خطای استاندارد یا بازه‌های اطمینان ۹۵٪ باشد. علاوه بر این، انتظار می‌رود که علاوه بر نتایج آزمون t زوجی، «اندازه اثر» (effect size) را نیز گزارش کنید. اندازه اثر مهم است. زیرا در حالی که آزمون t زوجی فقط به شما می گوید که آیا تفاوت بین میانگین های گروه “واقعی” است یا نه (یعنی در جامعه متفاوت است)، اما “اندازه” تفاوت را به شما نمی گوید. یک روش جداگانه‌ای در Minitab برای انجام این کار وجود دارد. در آینده در مورد آن بحث خواهیم کرد.