همبستگی حاصل‌ضرب-گشتاور پیرسون (Pearson’s Product-Moment Correlation) با استفاده از Minitab

پری کرمی
مارس 12, 2023
بدون دیدگاه

همبستگی پیرسون با استفاده از Minitab

مقدمه

همبستگی حاصل‌ضرب-گشتاور پیرسون (Pearson’s Product-Moment Correlation) که اغلب با عنوان همبستگی پیرسون بیان می گردد، برای ارزیابی قدرت و جهت ارتباط بین دو متغیر پیوسته که به صورت خطی مرتبط هستند استفاده می شود. ضریب آن که با r نشان داده می شود، قدرت و جهت این رابطه را نشان می دهد و می تواند از -1 برای یک رابطه کاملا خطی منفی تا +1 برای یک رابطه کاملا خطی مثبت متغیر باشد. مقدار 0 (صفر) نشان می دهد که هیچ رابطه ای بین دو متغیر وجود ندارد.

برای مثال، می‌توانید از همبستگی پیرسون استفاده کنید تا بفهمید آیا ارتباطی بین نمره امتحان و مدت زمان مرور درسی وجود دارد یا نه؟. در این مثال، دو متغیر «نمره امتحان» و «مدت زمان مرور درسی»هستند. اگر ارتباط مثبت و قوی وجود داشت، می‌توانیم بگوییم که زمان بیشتری که صرف مرور درسی می‌شود با نمره بالاتر امتحان مرتبط است.

در این آموزش، نحوه انجام همبستگی پیرسون با استفاده از Minitab و همچنین تفسیر و گزارش نتایج این آزمون را به شما نشان می‌دهیم. با این حال، قبل از اینکه شما را با این روش آشنا کنیم، باید فرضیات مختلفی را که داده‌های شما باید رعایت کنند تا همبستگی پیرسون به شما نتیجه معتبری بدهد، بدانید. در ادامه به این فرضیات می پردازیم.

فرضیات

همبستگی پیرسون دارای چهار فرض است. شما نمی توانید اولین مورد از این فرضیات را با Minitab آزمایش کنید زیرا به طراحی مطالعه شما و انتخاب متغیرها مربوط می شود. با این حال، باید این فرض را بررسی کنید. اگر این فرض برآورده نشود باید به جای همبستگی پیرسون از آزمون آماری دیگری استفاده کنید. فرض شماره 1 در زیر توضیح داده شده است:

فرض شماره 1:

دو متغیر شما باید در سطح پیوسته اندازه گیری شوند (یعنی متغیرهای فاصله ای (interval) یا نسبتی (ratio) هستند). نمونه‌هایی از این متغیرهای پیوسته عبارتند از: ارتفاع، دما، حقوق و دستمزد، زمان، هوش، سن، نمره امتحان، توان خروجی، میزان فروش و غیره.

توجه: اگر هر یک از دو متغیر شما در مقیاس ترتیبی اندازه گیری شد، باید به جای همبستگی پیرسون از همبستگی اسپیرمن (Spearman’s correlation) استفاده کنید. نمونه‌ای از متغیرهای ترتیبی عبارتند از مقیاس لیکرت (مثلاً مقیاس 7 درجه‌ای از «کاملاً موافقم» تا «کاملاً مخالفم» می باشد.

فرضیات شماره 2، 3 و 4 مربوط به ماهیت داده های شما هستند و می توان آنها را با استفاده از Minitab بررسی کرد. باید این فرضیات را بررسی کنید، در غیر این صورت، نتایجی که هنگام اجرای همبستگی پیرسون به دست می‌آورید ممکن است معتبر نباشند.

فرض شماره 2:

باید یک رابطه خطی بین دو متغیر شما وجود داشته باشد. چندین راه برای بررسی رابطه خطی وجود دارد. با این حال، پیشنهاد می کنیم با استفاده از Minitab یک Scatterplot ایجاد کنید، و دو متغیر را نسبت به یکدیگر رسم کنید. سپس می توانید به صورت بصری میزان خطی بودن نمودار پراکندگی را بررسی کنید. اگر رابطه نمایش داده شده در نمودار پراکنده شما خطی نباشد، یا باید داده های خود را “تبدیل” (transform) کنید یا به جای آن یک همبستگی اسپیرمن را اجرا کنید.

فرض شماره 3:

نباید نقاط پرت (outliers) قابل توجهی وجود داشته باشد. نقطه پرت به یک داده در مجموعه داده های شما است که از الگوی معمول پیروی نمی کند. پیرسون نسبت به نقاط پرت خیلی حساس است. این نقاط می تواند تأثیر بسیار زیادی بر روی خط بهترین تناسب (line of best fit) و ضریب همبستگی پیرسون داشته باشد، که در نهایت منجر به نتیجه گیری بسیار اشتباه در مورد داده های شما خواهد شد. بنابراین، بهترین کار این است که هیچ نقطه‌ی پرتی وجود نداشته باشد یا به حداقل برسد. خوشبختانه، می‌توانید در Minitab نمودارهای پراکنده ایجاد کنید تا نقاط پرت احتمالی را شناسایی کنید.

فرض شماره 4:

متغیرهای شما باید تقریباً به طور نرمال توزیع شوند. برای ارزیابی معنی‌داری آماری همبستگی پیرسون، باید نرمالیته دو متغیره (bivariate normality) داشته باشید. اما ارزیابی این فرض دشوار است. بنابراین روش ساده‌تر برای ارزیابی نرمال بودن، بهتر است هر متغیر به طور جداگانه بررسی شود. این کار را می توان با استفاده از آزمون Shapiro-Wilk برای بررسی نرمالیته انجام دهید.

در عمل، بررسی این فرضیات احتمالاً وقت بیشتری را هنگام انجام همبستگی پیرسون می‌گیرد. با این حال، کار سختی نیست و Minitab تمام ابزارهای مورد نیاز برای انجام این کار را در اختیار شما قرار می دهد.

در بخش بعدی، روش Minitab مورد نیاز برای انجام همبستگی پیرسون را با فرض اینکه هیچ فرضی نقض نشده است، نشان می‌دهیم. ابتدا، مثالی را که برای توضیح روش همبستگی پیرسون در Minitab استفاده کرده ایم، را ارائه می‌کنیم.

مثال

یک مربی می خواهد تعیین کند که آیا نمرات امتحانات دانش آموزان با مدت زمان مرور درسی مرتبط است یا خیر. برای مثال، وقتی دانش‌آموزان زمان بیشتری را صرف مرور درسی می‌کنند، آیا نمره امتحان آنها افزایش یافته است (یعنی رابطه مثبت) یا برعکس آن اتفاق افتاده است (یعنی رابطه منفی)؟ به این ترتیب، نمرات در یک امتحان ریاضی در مقیاسی از 0 تا 100 اندازه گیری شد و مقدار زمان صرف شده برای مرور درسی بر حسب ساعت اندازه گیری شد.

برای انجام آنالیز، محقق 40 دانش آموز را انتخاب کرد. مقدار مدت زمان مرور درسی (یعنی متغیر، Revision time) و نمرات امتحان (یعنی متغیر، Exam score) برای همه 40 شرکت‌کننده ثبت شد. محقق با بیان متغیرها، می خواست نمره امتحان و مدت زمان مرور درسی را به هم مرتبط کند. برای تعیین اینکه آیا بین نمره امتحان و مدت زمان مرور درسی رابطه آماری معناداری وجود دارد یا خیر از همبستگی پیرسون استفاده شد.

توجه: مثال و داده های استفاده شده برای این آموزش ساختگی هستند.

تنظیمات در Minitab

در Minitab دو متغیر خود را در دو ستون اول (C1 و C2) وارد کردیم. زیر ستون C1 نام متغیر Exam score و در زیر ستون C2 نام دومین متغیر یعنی Revision time را به صورت زیر وارد کردیم. در نهایت نمرات Exam score را در ستون Exam score و مدت زمان مرور درسی (برحسب ساعت) را در ستون Revision time وارد کردیم. این مراحال در زیر نشان داده شده است:

توجه: مهم نیست که کدام یک از دو متغیر خود را در C1 یا C2 وارد کنید.

مراحل آزمون در Minitab

در این بخش به شما نشان می‌دهیم که چگونه داده‌های خود را با استفاده از همبستگی پیرسون در Minitab آنالیز کنید. البته به شرطی که چهار فرض گفته شده در بخش فرضیات، نقض نشده‌ باشند. بنابراین، سه مرحله مورد نیاز برای اجرای همبستگی پیرسون در Minitab در زیر نشان داده شده است:

مرحله (1)

همانطور که در زیر نشان داده شده است، روی

Stat > Basic Statistics > Correlation…

در منوی اصلی کلیک کنید:

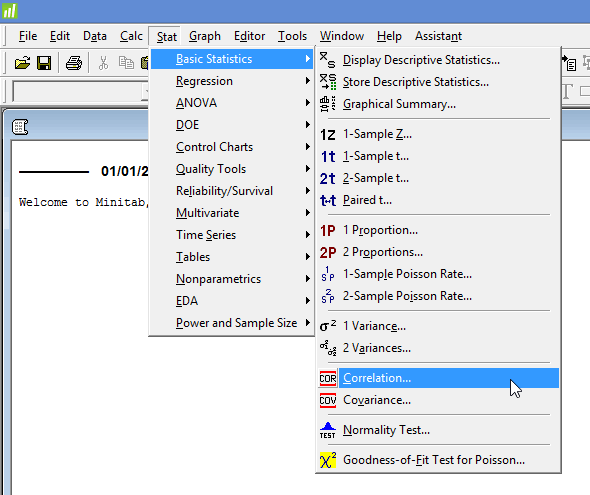
با پنجره ی Correlation زیر مواجه خواهید شد:

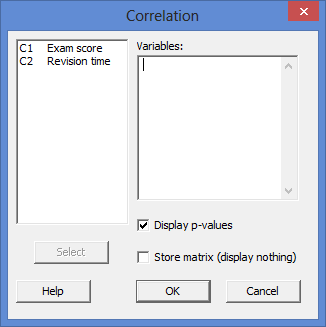
توجه: همانطور که در زیر نشان داده شده است، در برخی از ورژن های Minitab یک کادر Method هم وجود دارد. مطمئن شوید که “همبستگی پیرسون” در این کادر انتخاب شود:

مرحله (2)

دو متغیر خود، Exam score و Revision time را از کادر سمت چپ اصلی (یعنی C1 Exam score و C2 Revision time) به کادر Variables منتقل کنید. در نهایت با پنجره ی زیر روبرو خواهید شد:

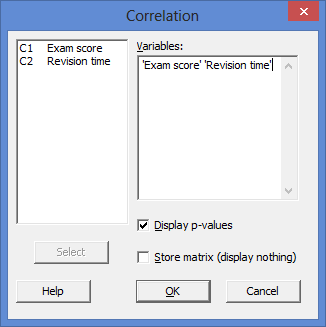
توجه: برای انتقال دو متغیر، ابتدا باید داخل کادر سمت چپ اصلی کلیک کنید و هر دو متغیر را انتخاب کنید (به عنوان مثال، C1 Exam score و C2 Revision time). این کار دکمه انتخاب را فعال می کند در حالی که قبل از آن بصورت غیر فعال بود. سپس، به سادگی دکمه را فشار دهید تا متغیر مورد نظر را به کادر Variables منتقل می‌کند.

مرحله (3)

بر روی دکمه OK کلیک کنید. خروجی Minitab در زیر نشان داده شده است.

خروجی همبستگی پیرسون در Minitab

خروجی Minitab برای همبستگی پیرسون در زیر نشان داده شده است:

خروجی شامل دو بخش مهم از اطلاعات است:

الف) ضریب همبستگی پیرسون، r. این قدرت ارتباط بین دو متغیر (یعنی نمره امتحان و زمان مرور درسی) را ارزیابی می کند.

ب) اهمیت آماری دو طرفه ضریب همبستگی پیرسون (یعنی p-value).

در این مثال، ضریب همبستگی پیرسون 0.853 است (یعنی خط “همبستگی پیرسون نمره امتحان و مدت زمان مرور درسی = 0.853”)، که با توجه به جدول زیر نشان دهنده همبستگی مثبت قوی بین دو متغیر نمره امتحان و مدت زمان مرور درسی است:

ضریب همبستگی	قدرت همبستگی
0.1 < \| r \| < .3	همبستگی کم و ضعیف
0.3 < \| r \| < .5	همبستگی متوسط
\| r \| > .5	همبستگی بزرگ و قوی

در این جدول | r | به معنای مقدار قدر مطلق r است. بنابراین، ضریب همبستگی پیرسون در این مثال (r = 0.853) نشان دهنده یک همبستگی قوی است. اگر در عوض، r = -.853 بود، شما باز هم یک همبستگی قوی، هرچند منفی، داشتید. این نتیجه نشان می دهد که زمان بیشتری که صرف مرور درسی می شود با نمرات امتحان بهتر (یعنی بالاتر) همراه است. همچنین می توانید ببینید که ضریب همبستگی پیرسون از نظر آماری به صورت p <.0005 معنی دار است (یعنی ردیف “P-Value = 0.000” که در واقع به معنای p <.0005 است)

گزارش خروجی همبستگی پیرسون

هنگامی که خروجی همبستگی پیرسون خود را گزارش می کنید، بهتر است که شامل موارد زیر باشد:

الف. مقدمه ای بر آنالیزی که انجام دادید.

ب. اطلاعات مربوط به نمونه شما (شامل مقادیر گمشده (missing values)).

ج. ضریب همبستگی پیرسون، r و درجه آزادی، که حجم نمونه منهای 2 است (در مثال بالا، برای حجم نمونه 40، درجه آزادی 38 خواهد بود).

د. سطح معناداری آماری (یعنی p-value) نتیجه شما.

با توجه به نتایج فوق می توان نتایج این تحقیق را به شرح زیر گزارش کرد:

همبستگی حاصل‌ضرب-گشتاور پیرسون برای ارزیابی رابطه بین نمره امتحان و زمان صرف شده برای مرور درسی در بین 40 دانش آموز اجرا شد. یک همبستگی مثبت قوی بین نمره امتحان و زمان صرف شده برای مرور درسی وجود داشت.

r(38) = .853, p < .0005

علاوه بر گزارش نتایج به شرح بالا، می توان از یک نمودار (به عنوان مثال، یک نمودار پراکنده) برای ارائه بصری نتایج استفاده کرد. این می تواند درک نتایج شما را برای دیگران آسان تر کند و به راحتی در Minitab تولید می شود.